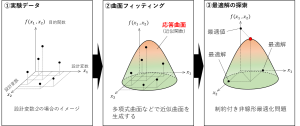
応答曲面法による最適化設計（第四回）
実験計画と実験

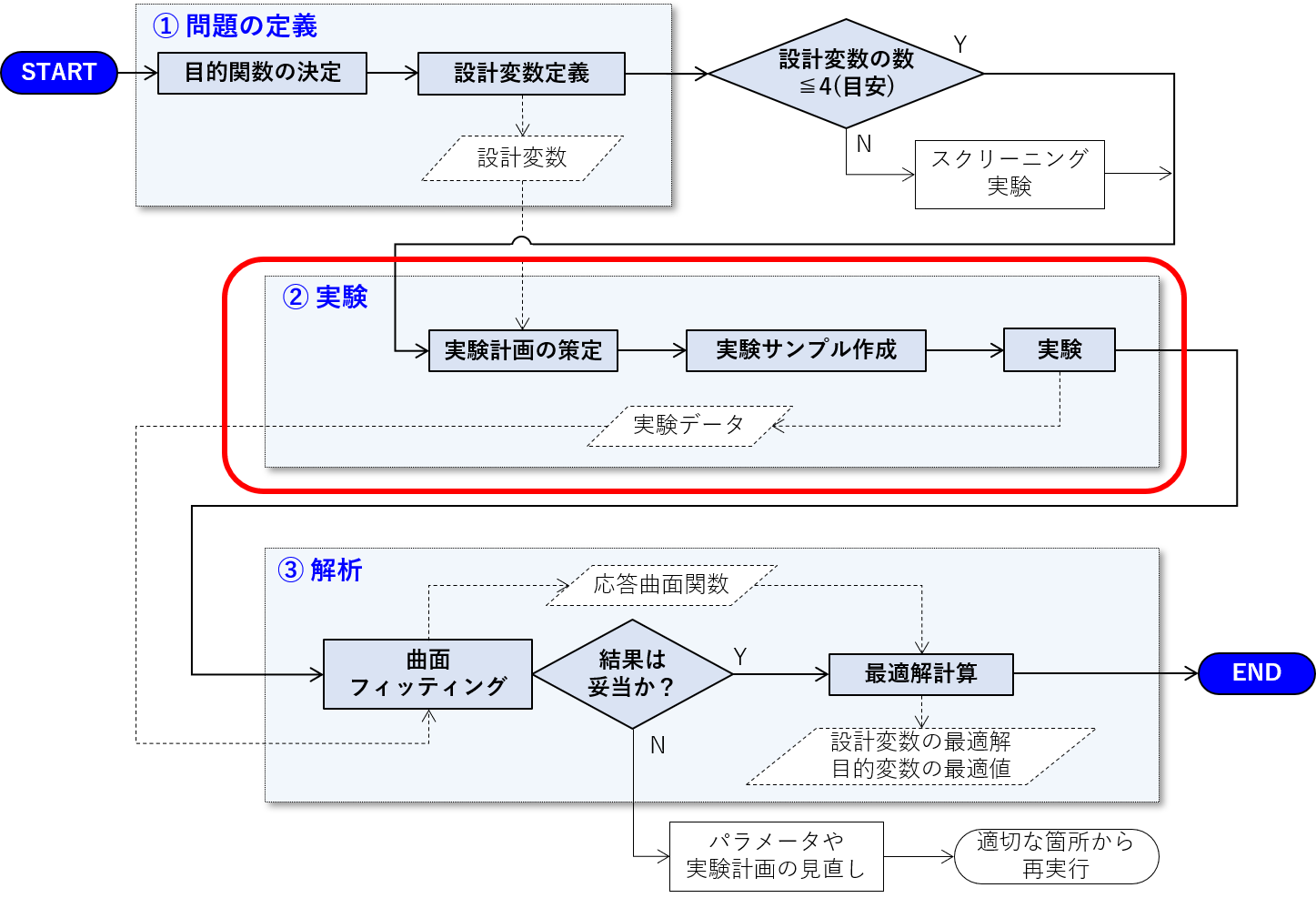
前回はスクリーニング実験について説明し、影響が大きいと思われる設計変数の絞り込みを行いました。これで、応答曲面法を本格的に適用する準備が整いました。今回は、フローチャートで下記の通り、曲面フィッティングのためのデータ収集＝実験について説明をします。

設計変数の基準化

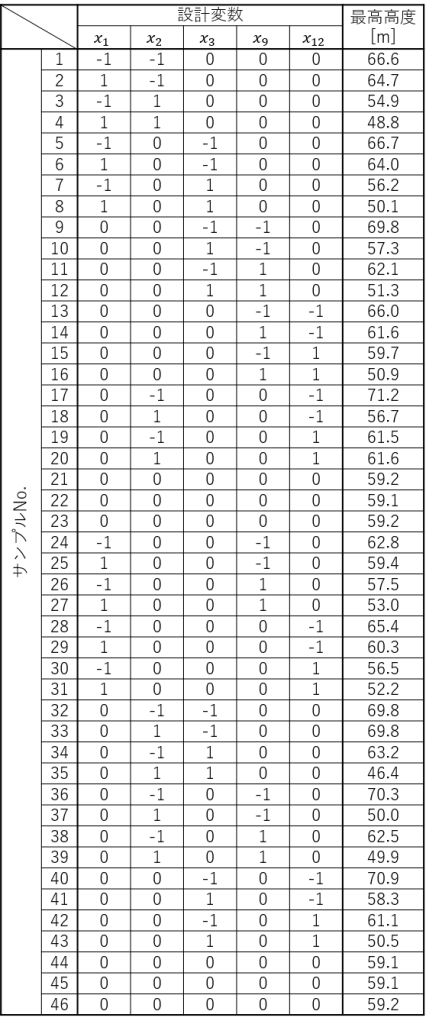
あらためて、デモ問題の設計変数のリストを見てみます。

各設計変数の上下限値が定義されていますが、数値の範囲は設計変数によってバラバラです。
異なる箇所の寸法値等なので当然ですが、応答曲面法ではこれが問題になることがあります。
応答曲面法では、設計変数の数値範囲はなるべく揃えるほうがベターです。

ここで、「基準化」という操作を行います。基準化は、各設計変数の下限値を-1、上限値を1にする変数変換です。変換は次式で行われます。

$$x_s=\displaystyle\frac{x-\displaystyle\frac{x_u+x_l}{2}}{\displaystyle\frac{x_u-x_l}{2}}$$

$$\begin{eqnarray}
x &:& 元の設計変数値\\
x_s &:& 基準化された設計変数値\\
x_u &:& 設計変数値の上限値\\
x_l &:& 設計変数値の下限値
\end{eqnarray}$$

実験計画の作成と曲面フィッティングの際は基準化された設計変数値を用います。もちろん、実験（シミュレーション）する際には、元の設計変数値を用いてサンプルを作成します。

基準化された設計変数の範囲は、以下のように図示が可能です。

• 設計変数が2個の場合：辺の長さが2の「正方形」の内側

• 設計変数が3個の場合：辺の長さが2の「立方体」の内側

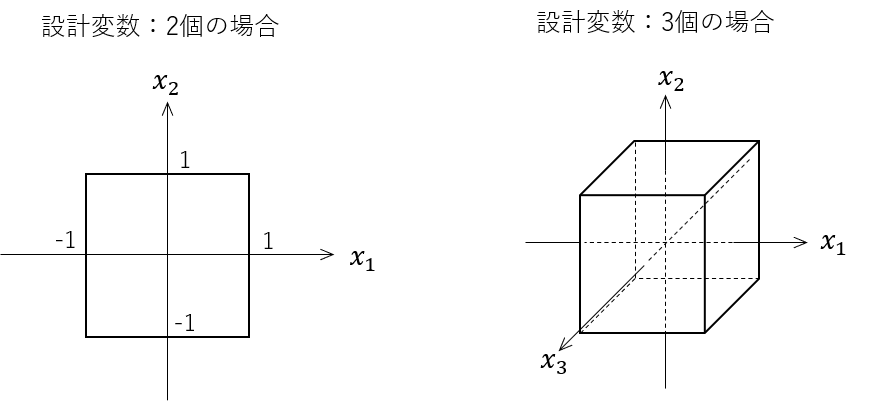
なお、設計変数が4個以上の場合は、多次元の立方体になり、図示することはできません。

実験計画

応答曲面法に適した実験計画とはどのようなものでしょうか。直感的に、基準化された設計変数の範囲内で均一に分布していると良さそうです。

応答曲面法では、主に「中心複合計画」と「Box-Behnken計画」のいずれかがよく用いられます。

中心複合計画（Central Composite Design: CCD）

設計変数が2および3個の場合の中心複合計画は、下のように図示できます。

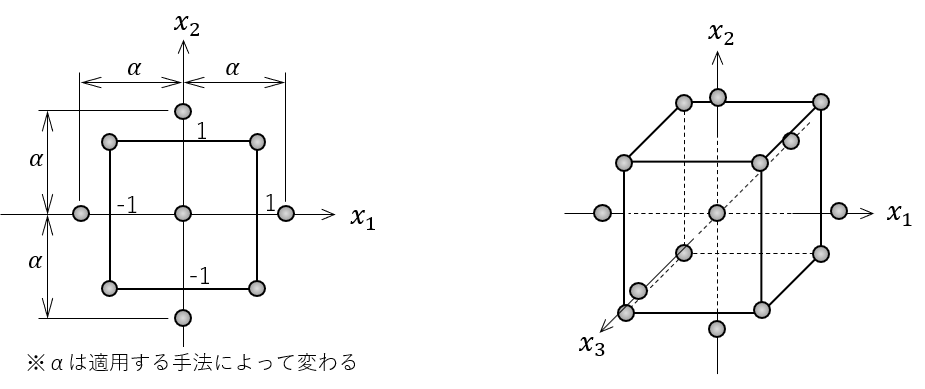
実験サンプルは、正方形または立方体の中心と各頂点、および外側の点です。外側の点までの距離\(\alpha\)には様々なバリエーションがありますが、今回は説明を省略します。

Box-Behnken計画（BBD）

設計変数が2および3個の場合のBox-Behnken計画は下のように図示できます。

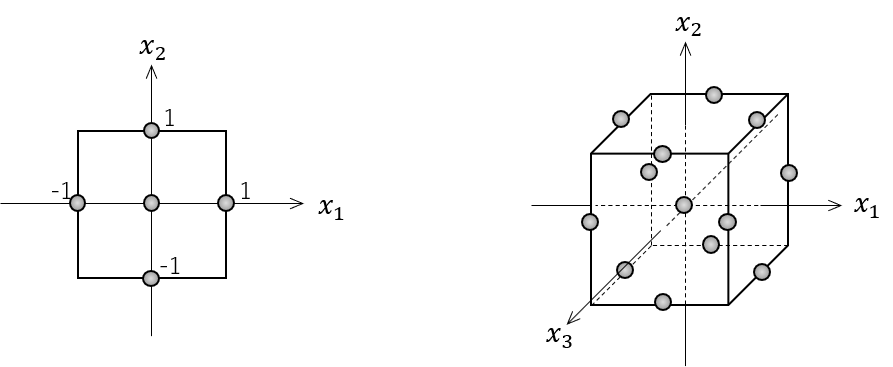
正方形または立方体の中心と、各辺の中点に実験サンプル点が配置されます。

どちらを使えばよいのか

中心複合計画とBox-Behnken計画の特徴を簡単に示すと、下記表のようになります。

2つの計画では、メリットとデメリットが相反しています。これから分かるように、どちらを用いるべきかについては、明確に決め方があるわけではありません。
実験（シミュレーション）に要する時間やサンプル作成の工数など、様々な状況を勘案して決めれば良いのです。

今回のデモ問題では、Box-Behnken計画を用いることにしました。
設計変数の数は5つなので、正方形や立方体で考えるのは一苦労です。これについても、スクリーニング実験のときと同じように、Rのライブラリなどを用いれば、簡単に実験計画を出力してくれます。

中心点の実験回数について

なお、実験にランダムな誤差がある場合、中心点の実験回数が曲面フィッティングの精度に影響を与えることが知られています。中心点の実験数は概ね3～4回程度行います。今回の飛翔シミュレーションは、ノイズを考慮している（風速に確率変数がある）ので、中心点の実験回数は3としました。

実験計画と実験結果

デモ問題の実験計画を以下に示します。全部で46回の実験計画になっています。また、スペースがもったいないので、シミュレーション結果もここで載せています。

余談

さて、実験計画の策定に当たっては、設計変数の上下限値を第2回記事で定義したものをそのまま適用しています。

ここで、第3回記事のスクリーニング実験の結果を再度見てみましょう。
要因効果図から、各設計変数の水準を最高高度を取る水準でシミュレーションした結果、かなりの改善が見られました。したがって、新たにこの水準の周辺で設計変数の範囲を再定義するという戦略も「あり」です。

しかし、設計実務においては、条件の再定義には慎重を期すべきです。
第1回記事でも書いたように、私はロケット工学や空気力学の分野では素人同然です。スクリーニング実験の結果（要因効果図）について、理論的な説明はできません。もし、理論的な説明が可能であれば、それに基づき設計変数の範囲を再定義してもよいと思います。今回はそうではないので、私自身で結果に責任を持つことはできないと判断し、再定義を見送りました。

もちろん、こういった判断に明確な正解・不正解はありません。しかし、判断の責任は常に設計者にあるということは肝に命じておかなければなりません。

まとめ

応答曲面法における実験計画について説明をしました。デモ問題においてはBox-Behnken計画を適用して実験（シミュレーション）計画を策定し、シミュレーションを実施しました。

次回はこのシミュレーション結果を用いて曲面フィッティングを実施し、応答曲面を導出します。そして、応答曲面上での最適値探索を行い、設計の締めまで説明します。