多目的最適化問題(第四回)
遺伝的アルゴリズムについて
いよいよ、多目的最適化問題の求解(パレートフロントの求解)について、説明する段階に来ました。
しかし、その前に、副題の通り「遺伝的アルゴリズム」について概要を説明します。多目的最適化問題の求解アルゴリズムである「NSGA-Ⅱ」は、遺伝的アルゴリズムを基本にしているからです。そのため、まずは「遺伝的アルゴリズムによる単目的最適化問題の最適化」について説明をします。
遺伝的アルゴリズムの概要
遺伝的アルゴリズムは、「メタヒューリスティックス手法」と呼ばれるカテゴリに分類されます。メタヒューリスティック手法とは、自然界の現象などの模倣を通じて経験的に問題を解く手法を総称したものです。遺伝的アルゴリズムは「進化的計算」などとも呼ばれ、生物の進化からヒントを得ていると言われています。
遺伝的アルゴリズムで単目的関数の最適化の概要を以下の図で説明します。
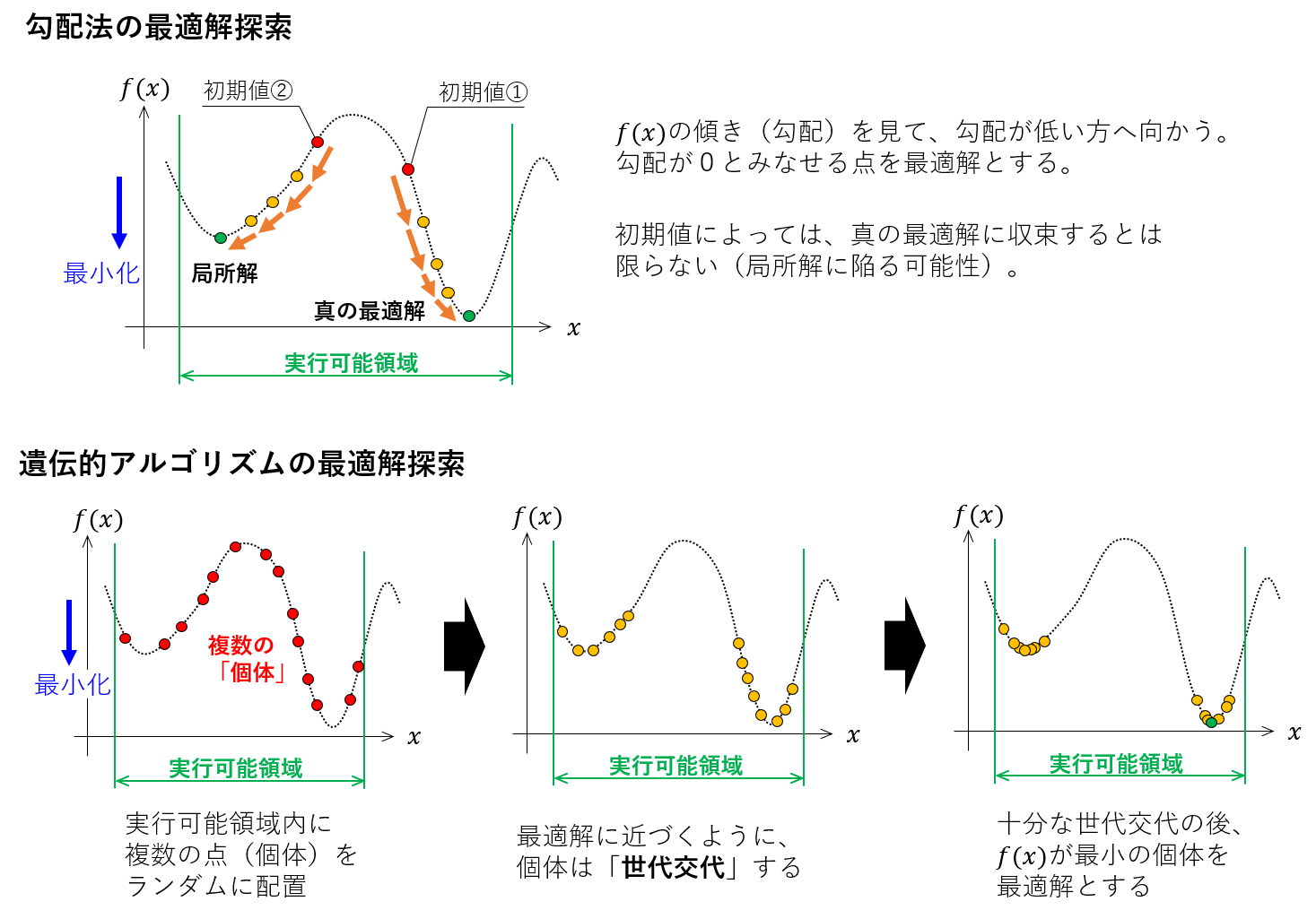
上段は「勾配法」という手法についての説明です。目的関数の傾き(勾配)を計算し、勾配の方向・大きさによって、より最適に近い解を探索して行くアルゴリズムです。原理は簡単で、今日でも最適化問題の求解によく利用されます。しかし、図に示すように、探索を開始する点(初期値)によっては、真の最適値にたどり着けない場合があります。
一方、下段が遺伝的アルゴリズムについて説明したものです。実行可能領域内に配置された複数の「個体」が、アルゴリズムのステップ毎に最適値を目指して「世代交代」するイメージです。どのように世代交代をさせるかが、遺伝的アルゴリズムの肝要です。
アルゴリズムのフローチャートは次の通りです。このように、世代交代は、①選択・②交叉・③突然変異の3つの操作によって行われます。
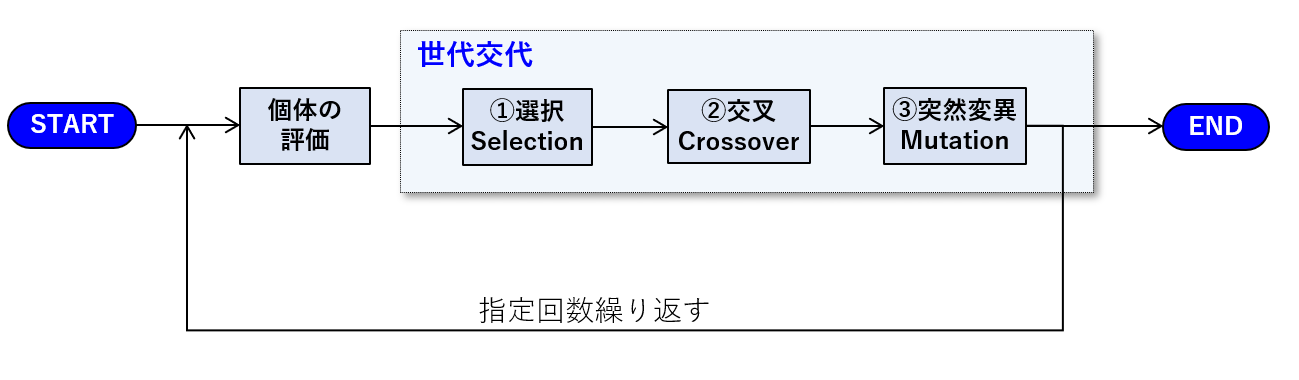
各々の操作には様々な方法が提案されていて、遺伝的アルゴリズムには多くのバリエーションがあります。以降では、代表的な方法について説明をします。
遺伝的アルゴリズムによる単目的関数の最適化
例題
ここからは、例題を用いて説明をします。次のような2変数1目的関数の最小化問題を考えます。
$$f(x_1 , x_2)=(x_1-1)^2+(x_2-0.6)^2+1$$
$$f(x_1 , x_2)→\rm{min}$$
なお、この目的関数の最小値は、\(x_1=1.0\)、\(x_2=0.6\)のときに、\(f(x_1 , x_2)=1.0\)となります。
遺伝子の設定と個体の評価
最初に、個体の設定を行います。
遺伝的アルゴリズムの個体は「遺伝子」という特徴量を持っています。例題のような最適化問題の場合、遺伝子には設計変数が当てられます。
アルゴリズムの開始時点では、個体の遺伝子情報(設計変数値)はランダムに決められます。また、個体数はあらかじめ設計者によって設定されます。
世代交代の操作には、「個体の評価値」を用いるものがあります。この場合の評価値は、「目的関数の値」になります。最小化問題の場合は、評価値が小さいほど、その個体は適合していることになります。
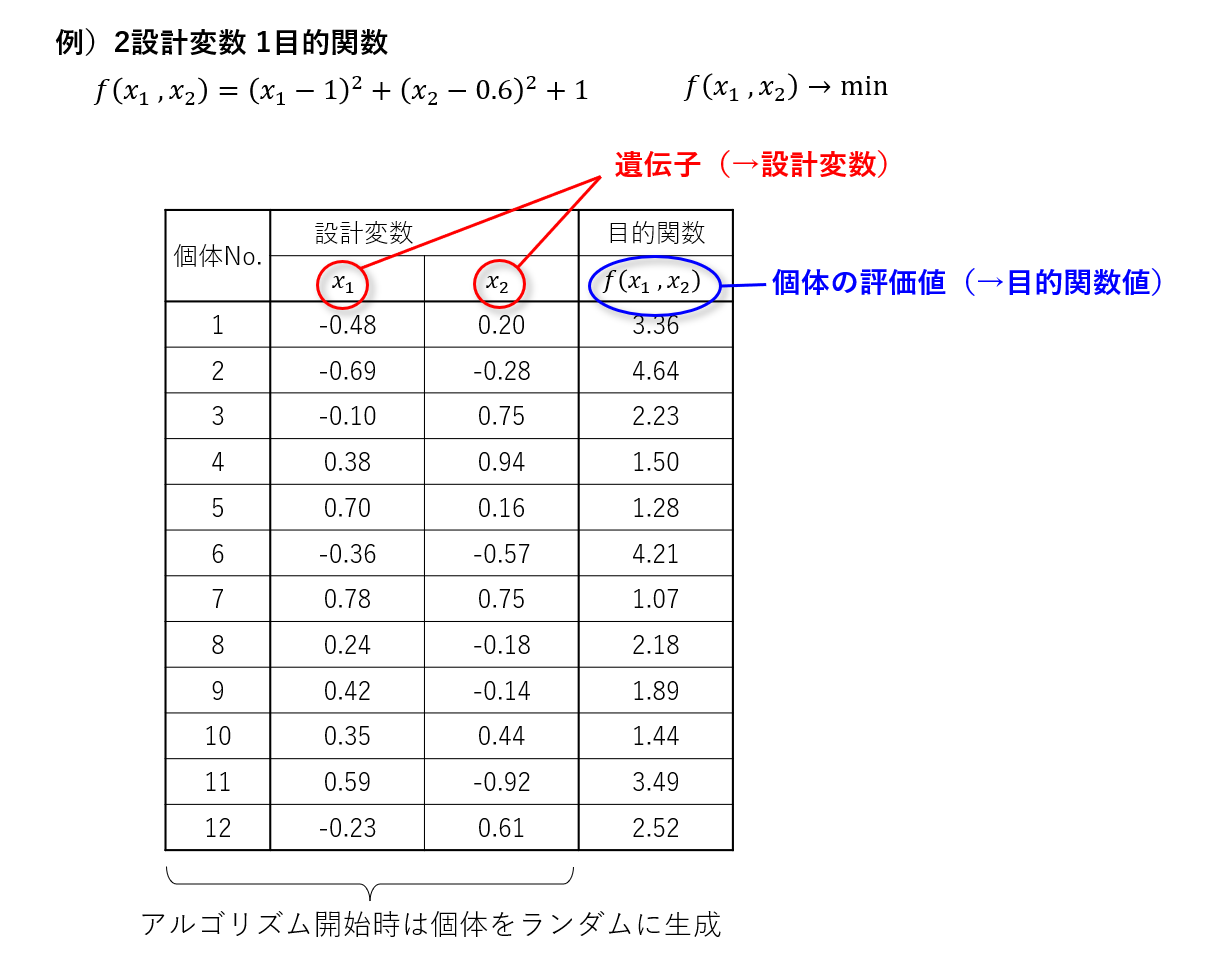
このように、実数で構成される遺伝子を「実数型」と呼ばれます。このほかに、0か1のみで表される「バイナリ型」などがあります。
世代交代の操作
①選択
「選択」の代表例として「トーナメント選択」があります。これは、次のように、個体群から指定数の個体をランダムに抽出し、これらの中で最も最適値に近い個体を残すという操作です。ランダム抽出にすることで、最適値から離れている個体も残る可能性があり、局所解に陥るリスクを低減しています。
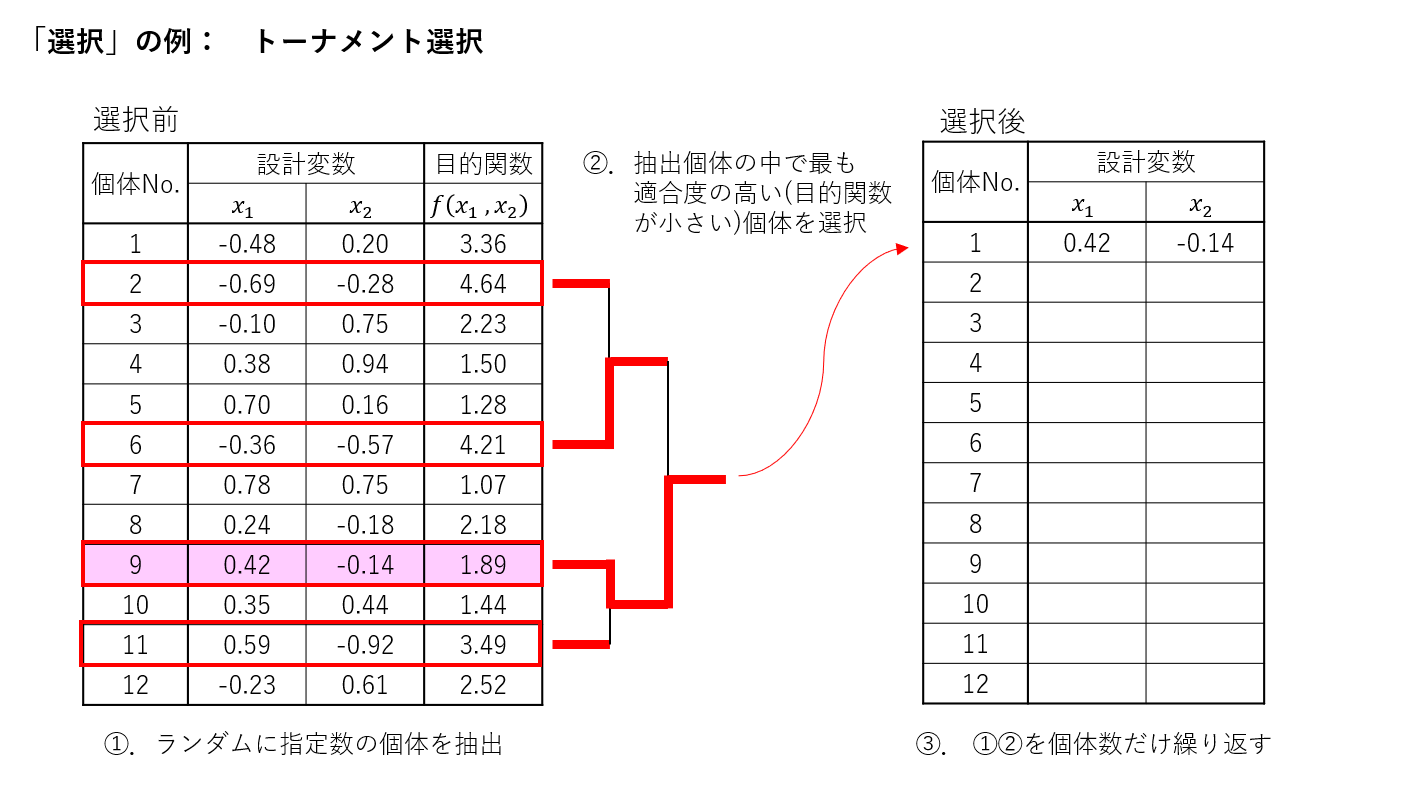
②交叉
「交叉」とは、親個体から子個体を生成する操作です。以下は、「ブレンド交叉(BLX-α)」と呼ばれる交叉操作です。2つの親個体から2つの子個体を生成します。\(\alpha\)はパラメータで、設計者が指定する必要があります。
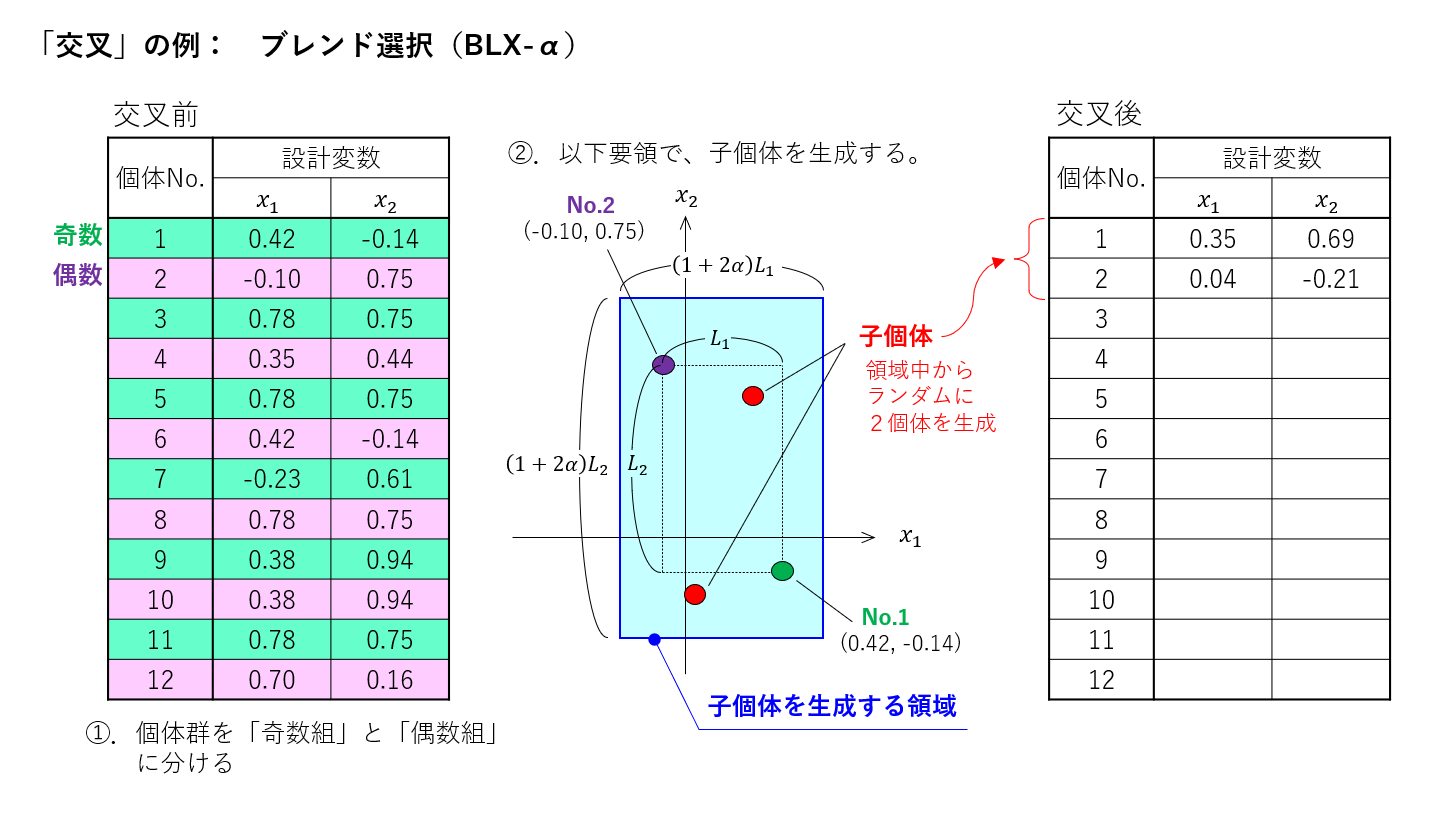
③突然変異
突然変異は、ある確率で個体を大きく変化させる操作です。確率は低いのですが、これを行うことによって、局所解に陥るリスクを低減します。突然変異操作の例として、「ガウシアン変異」を以下にて説明します。正規分布の標準偏差\(\sigma\)がパラメータです。
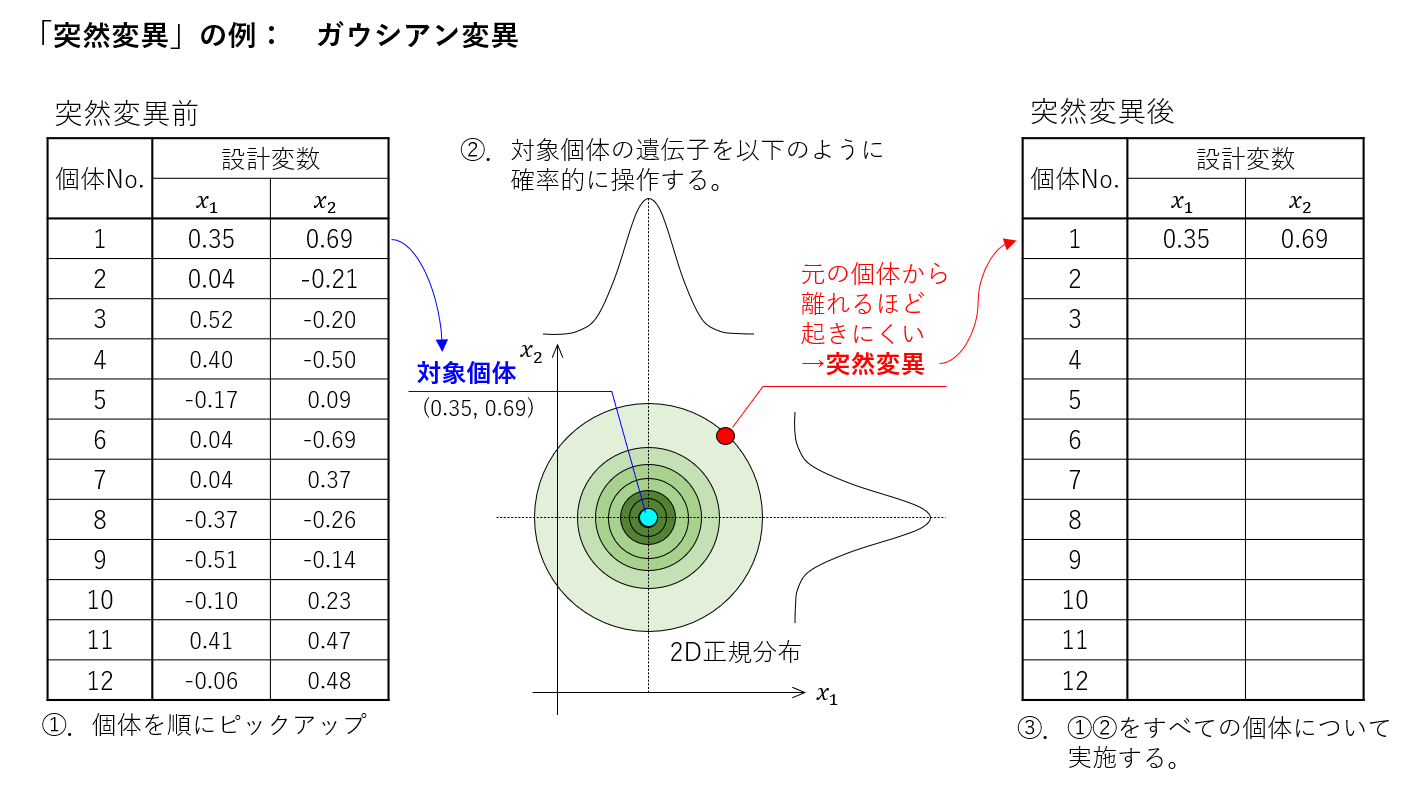
例題の求解
実際に、例題を遺伝的アルゴリズムで解いてみます。個体数は\(100\)、世代交代の繰り返し数を\(100\)としてみます。計算には、Pythonのライブラリdeapを使用しています。プログラムの説明については詳細を省略します。
結果は次の通りです。
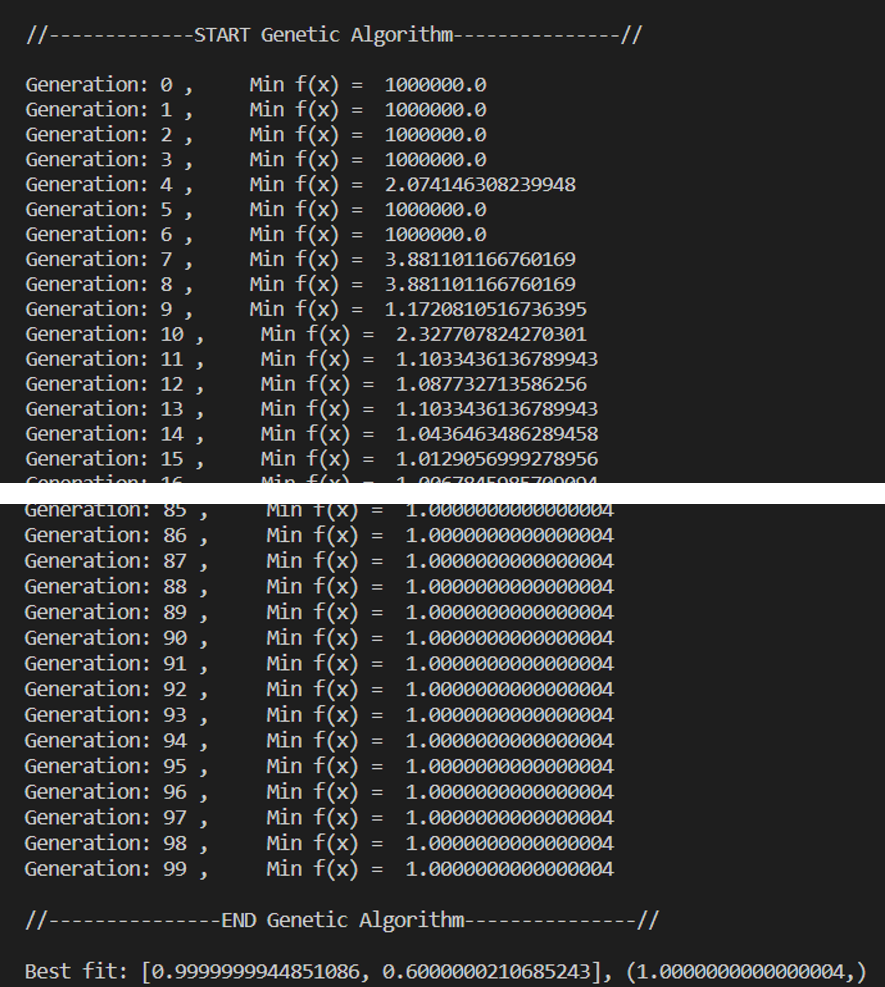
世代交代時における、評価値(目的関数の値)が表示され、最後の"Best fit"にて、指定数の世代交代終了時に最も評価の高い個体の情報を示しています。
結果は、\(x_1=1.0\)、\(x_2=0.6\)のときに、\(f(x_1 , x_2)=1.0\)ですが、小数点以下の小さいオーダーでは完全に一致していません。
このように、遺伝的アルゴリズムではある程度の誤差が出てきます(これは、遺伝的アルゴリズムのというよりは、メタヒューリスティック手法の特徴)。
まとめ
多目的最適化問題の求解のアルゴリズムの基になっている「遺伝的アルゴリズム」について説明をしました。
遺伝的アルゴリズムは、実行可能領域内で、複数の「個体」が最適値に近づくように「世代交代」することで、局所解に陥らずに最適値を得るアルゴリズムです。
世代交代は、「選択」「交叉」「突然変異」の3操作によって行われます。
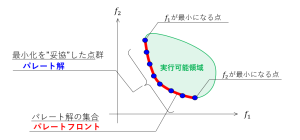
次回では、遺伝的アルゴリズムを多目的最適化問題に適用したアルゴリズムについて説明します。先にイメージを述べると、以下のようになります。
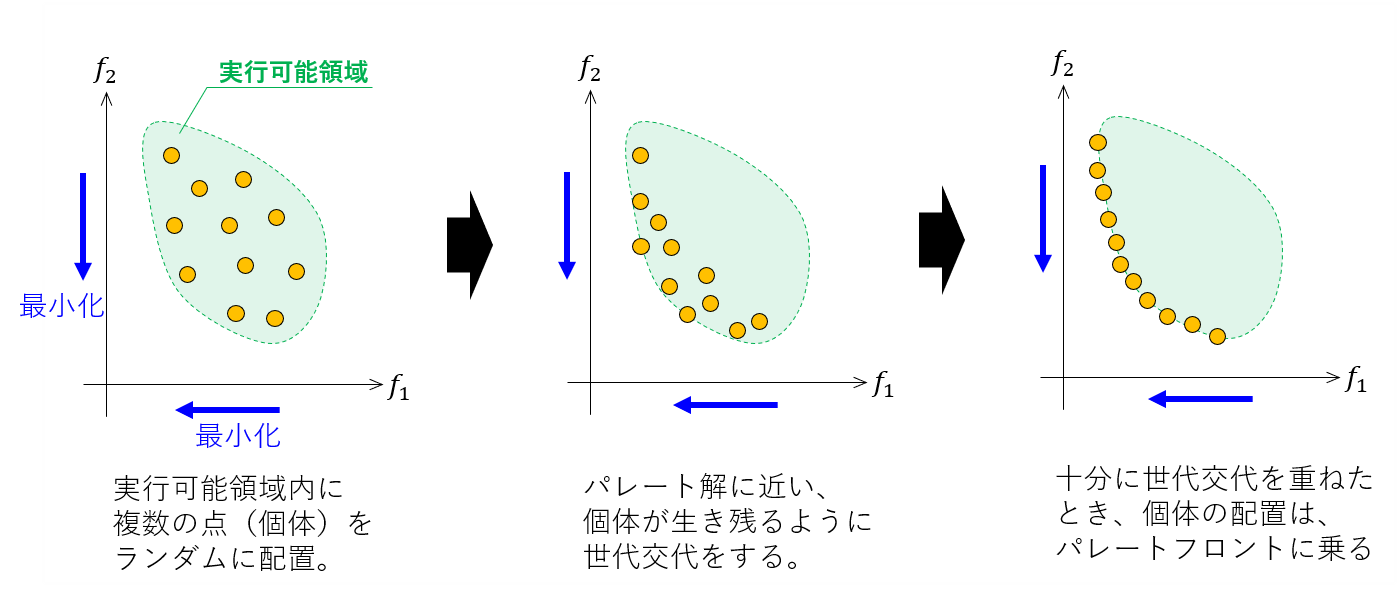
世代交代の過程を追っていくと、個体群はパレートフロントを目指して移動しているように見えます。このような世代交代を行うには、個体評価・選択・交叉・突然変異をどのように操作すればよいのでしょうか。詳細は次の記事にて説明をします。