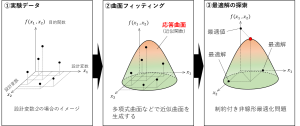
応答曲面法による最適化設計（第五回）
曲面フィッティングと最適解探索

前回は実験計画と実験について説明しました。

今回は、応答曲面法のクライマックスです。前回の実験データを使って、応答曲面のフィッティングと曲面上での最適値探索（最適解計算）について説明をします。

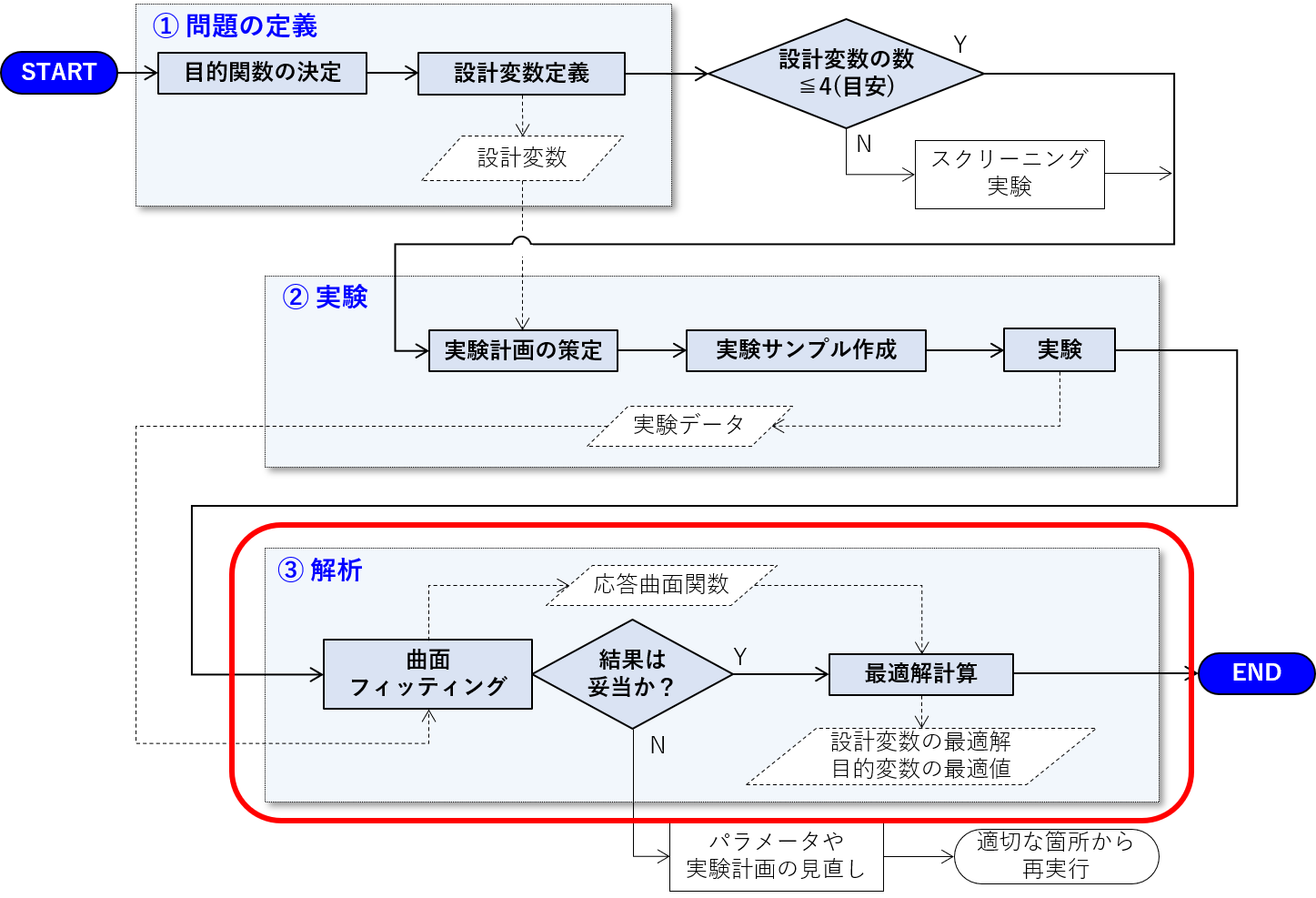
曲面フィッティング

第一回の記事で、応答曲面は何らかの数式（関数）に従うと書きました。では、どのような関数が用いられるのでしょうか。

実際の実務では、「2次関数」と「RBFネットワーク」が良く使われています。

RBFネットワークには調整パラメータがあり、2次関数に比べて扱いが難しいものとなっています。
また、設計実務では、2次関数で十分なことが多いです。
よって、ここでは、2次関数による曲面フィッティングを説明します。

余談ですが、RBFネットワークは、名前に「ネットワーク」とありますが、これは「ニューラルネットワーク」の一種だからです。ニューラルネットワークは「機械学習」と相性が良いモデルです。RBFネットワークにも、「実験データの追加取得による精度向上」などといった拡張性があります。
いずれ、これは記事にしようと思っています。

2次関数によるフィッティング

2次関数とは、変数の2乗の項を含む関数です。具体的な応答曲面の関数式は次の通りです。

$$\begin{eqnarray}
f(x_1,\cdots,x_n)&=&\beta_{11}{x_1}^2+\cdots+\beta_{nn} {x_n}^2 \\&&+\beta_{12}{x_1}{x_2}+\beta_{13}{x_1}{x_3}+\cdots+\beta_{n-1 n} {x_{n-1}}{x_{n}}\\&&+\beta_{1}x_1+\cdots+\beta_{n}x_n\\&&+\beta_0
\end{eqnarray}$$

右辺1行目が「二乗項」です。また、2行目は「交差項」と呼び、2つの設計変数の組み合わせの数だけあります。3行目が単数項で、4行目が定数です。

係数値の導出

二乗項と交差項の計算

まず、下準備として、実験データを以下のように加工します。文章だと少し分かりづらいかもしれません。下の図を見ながら読み進めて頂くと良いと思います。

①設計変数の二乗項の計算

実験計画の各サンプルにおいて、基準化された各設計変数の値を2乗値を計算します。

②設計変数の交差項の計算

実験計画の各サンプルにおいて、基準化された各設計変数の交差項の全組み合わせを計算します。

③要素1の追加列

すべての要素が1の列を追加します。

以下、デモ問題の場合の計算例です。

最小二乗法による係数値の導出

上記の二乗項と交差項を追加した実験データの表において、説明変数に関係する領域をまとめて、行列\(\boldsymbol{X}\)とします。また、実験データの列を、列ベクトル\(\boldsymbol{y}\)とします。

そして、係数を並べた、次のような列ベクトル\({\boldsymbol{\beta}}\)を定義します。

$$\boldsymbol{\beta}={\lbrack \begin{array}{cccc}
\beta_{1}\cdots\beta_{n}&,&
\beta_{11}\cdots\beta_{nn}&,&
\beta_{12},\beta_{13}\cdots\beta_{n-1n}&,&
\beta_0 \end{array}\rbrack}^T$$

\(\boldsymbol{X}\)、\(\boldsymbol{y}\)、\(\boldsymbol{\beta}\)を用いると、応答曲面の関数式は以下のようになります。

$$\boldsymbol{y}=\boldsymbol{X}\boldsymbol{\beta}$$

これは\(\boldsymbol{\beta}\)を未知数とする連立一次方程式です。\(\boldsymbol{\beta}\)は、両辺に左から\(\boldsymbol{X}\)の一般化逆行列を掛けることで求められます。すなわち、次式の通りです。

$$\boldsymbol{\beta}={(\boldsymbol{X}^T\boldsymbol{X})}^{-1}\boldsymbol{X}^T\boldsymbol{y}$$

一般化逆行列の計算などは手計算での実行は大変ですが、計算機を使えば一瞬です。頑張ればExcelでも可能です。

デモ問題について、応答曲面の関数式は以下のようになりました。

$$\begin{eqnarray}
f(x_1,\cdots,x_n)&=&-1.14{x_1}^2+1.26{x_2}^2+1.23{x_3}^2-0.72{x_4}^2+0.97{x_5}^2 \\
&&-1.05{x_1}{x_2}-0.85{x_1}{x_3}-0.28{x_1}{x_4}+0.20{x_1}{x_5}\\
&&-4.20{x_2}{x_3}+1.93{x_2}{x_4}+3.65{x_2}{x_5}+0.43{x_3}{x_4}\\
&&+0.50{x_3}{x_5}-1.10{x_4}{x_5}\\
&&-2.13x_{1}-5.73x_{2}-6.31x_{3}-2.91x_{4}-3.53x_{5}\\
&&+59.15
\end{eqnarray}$$

応答曲面の視覚化

さて、「曲面」というからには何らかの形があるはずです。

しかし、設計変数の数は5つ。応答曲面は6次元空間に浮かぶ5次元の超平面です。図示することも想像することもできませんが、どうにかして雰囲気だけでもつかめないでしょうか。

考えられるのは、5つの設計変数の内、2つだけに注目し3次元プロットを作成することです。
つまり、2つの設計変数を選択し、それ以外の設計変数の値は0にでもしておき、3次元プロットを作成するのです。設計変数の選択の組み合わせは、10通り（\(={}_5 C_2\)）あるので、10個の3次元プロットが作成できます。

3次元のプロットを並べても見づらいので、色によって高低を表現したコンター図を作成してみました。青～緑～茶となるに伴い、関数値が大きくなります。地形図と同じです。

また、赤い四角形は設計変数の範囲を示しています（これらのプロットの設計変数値は基準化前の元の数値です）。

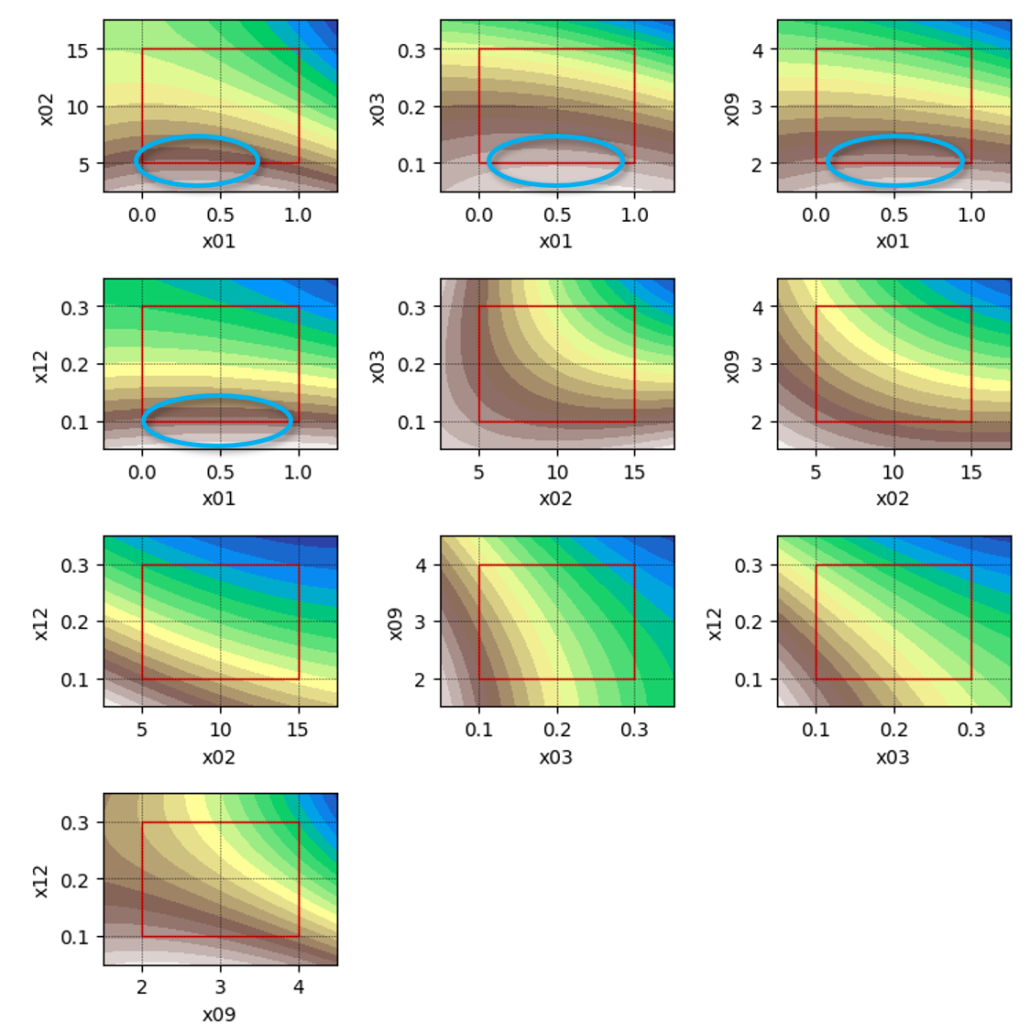
視覚化してわかること

さて、これらのプロット図から何か分かることはないでしょうか。

青い丸で囲った領域に注目してください。設計変数\(x_1\)のみ、設計変数の定義範囲内でゆるやかな凸になる箇所があるように見えます。

一方、それ以外の設計変数にはこのような領域は見られません（\(x_2\)がやや凸に見えますが、\(x_1\)ほど顕著ではありません）。このことから、\(x_1\)は、定義範囲内で最適値を持つことが予想※されます。

※これらのプロットは多次元の応答曲面の一部分のみを切り取ったものであり、本当の形状は分かりません。したがって、あくまで「予想」です。

最適値探索

「応答曲面上で最適値がどこにあるのか」を解く問題は、「制約条件付き最適化問題」の解法を適用して求めます。ここでいう制約条件とは、設計変数の上下限範囲のことです。

つまり、問題を定式化すると次のようになります。

$$\begin{eqnarray}
f(x_1,\cdots,x_n)&=&\beta_{11}{x_1}^2+\cdots+\beta_{nn} {x_n}^2 \\&&+\beta_{12}{x_1}{x_2}+\beta_{13}{x_1}{x_3}+\cdots+\beta_{n-1 n} {x_{n-1}}{x_{n}}\\&&+\beta_{1}x_1+\cdots+\beta_{n}x_n\\&&+\beta_0
\end{eqnarray}$$

$$\begin{cases}
\begin{eqnarray}
-1\text{≦}&x_1&\text{≦}1\\
-1\text{≦}&x_2&\text{≦}1\\
&\vdots&\\
-1\text{≦}&x_n&\text{≦}1\\
\end{eqnarray}
\end{cases}$$

$$f(x_1,\cdots,x_n)\rightarrow \text{min or max} $$

この問題の解法は様々なものがあり、これだけで「最適化問題」の一ジャンルを築いています。本記事では解法に関する詳細の説明は省きます。
SQP(逐次二次計画法)と呼ばれる手法で応答曲面の最適値を求解した結果、以下のようになりました。

$${\lbrack \begin{array}{ccccc}
x_{1},&x_2,&x_3,&x_4,&x_5\end{array}\rbrack} =
{\lbrack \begin{array}{ccccc}
0.466,&5.0,&0.1,&2.0,&0.1\end{array}\rbrack}$$

数値は基準化前の単位に戻しています。予想通り、\(x_1\)は定義範囲内で最適解を持ち、それ以外の設計変数は定義範囲の境界で最適解となりました。また、このときの最適値は81.6[m]になりました。

確認実験

設計変数の最適解で飛翔シミュレーションを実施してみました。結果は以下の通りになりました。

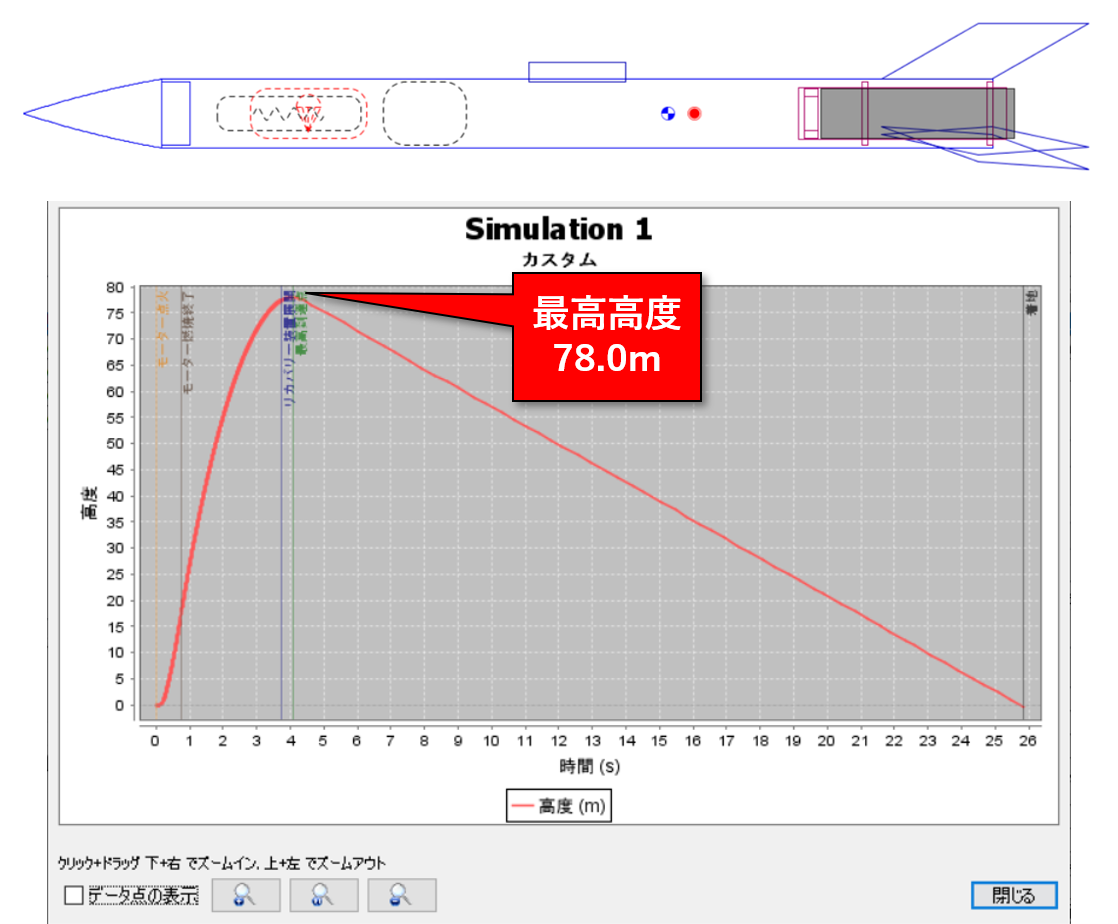
最高高度は78.0mです。応答曲面上の最適値と比べて若干低い値ですが、応答曲面はあくまで近似値なのでこれは致し方ありません。

ですが、スクリーニング実験時に出てきたベンチマークよりも、わずか0.2mですが良い結果になっています。競技を想定していますから、少しでも高い高度に達する方が良い設計と言えるでしょう。

あらためて、設計前のサンプルファイルと設計後の形状を比べてみます。
ノーズコーンは短く、フィンは全体的に小型化され後退量が大きくなっています。

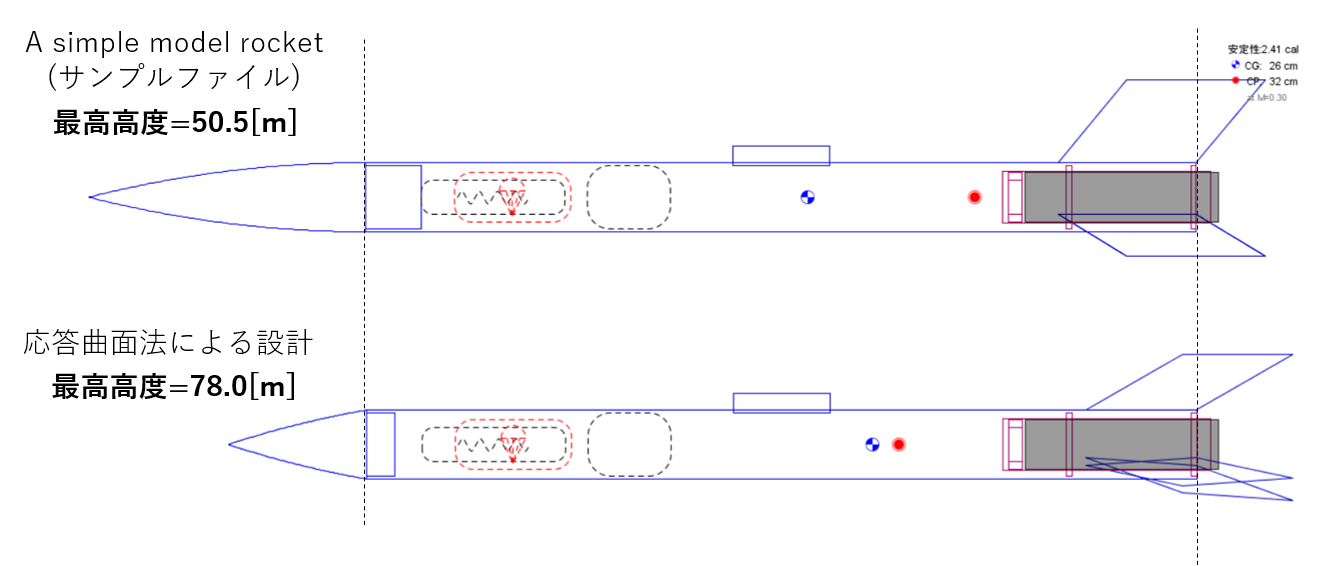
しかし、残念ながら「こういったことがなぜ飛翔高度UPにつながるのか」は、今の私には分かりません。ここまで出した結果は、言わば「数字をこねくり回した結果」でしかありません。

これ以上の改善設計は、OpenRocketに関する論文を読んでからにしようと思います。

まとめ

ここまでで一通り、応答曲面法による最適化設計について説明をしました。処理すべき情報が多く実験回数も多いので、実施するのは確かに大変です。

しかし、近似とは言え、目的関数の曲面形状が分かることは大変有用です。例えば、今回のデモ問題の場合、一応の最適解が得られたものの、その解は「当初定義した範囲の境界上」に位置しているものがほとんどでした。つまり、定義範囲を見直すことでさらに性能を上げられる可能性もあることが示唆されます。

記事はここで筆を置きますが、求解だけでなく次につながる一手も見出すことも設計者の仕事です。