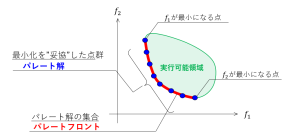
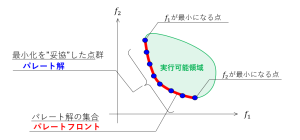
多目的最適化問題(第三回)
RBFネットワークによる応答曲面法(後半)
前回は、多目的最適化問題を解く(パレートフロントを求める)ための前段階である、目的関数の数式化(RBFネットワークによる応答曲面法)について説明をしました。
その後編である今回は、実際に設計対象について手法を適用し、応答曲面関数を求める作業をしていきます。詳しい計算式などは前回を参照ください。
デモ問題(設計対象)
デモ問題についておさらいしておきます。
ロバストパラメータ設計の際に用いた設計対象について、「感度」と「SN比」の2つの特性の最適化を狙います。すなわち、目的関数は「感度」と「SN比」です。
今回実施することは、感度とSN比の各々について、RBFネットワークの各パラメータを求めていくことです。
実験(シミュレーション)サンプルと、感度・SN比のデータは以下の通りです。
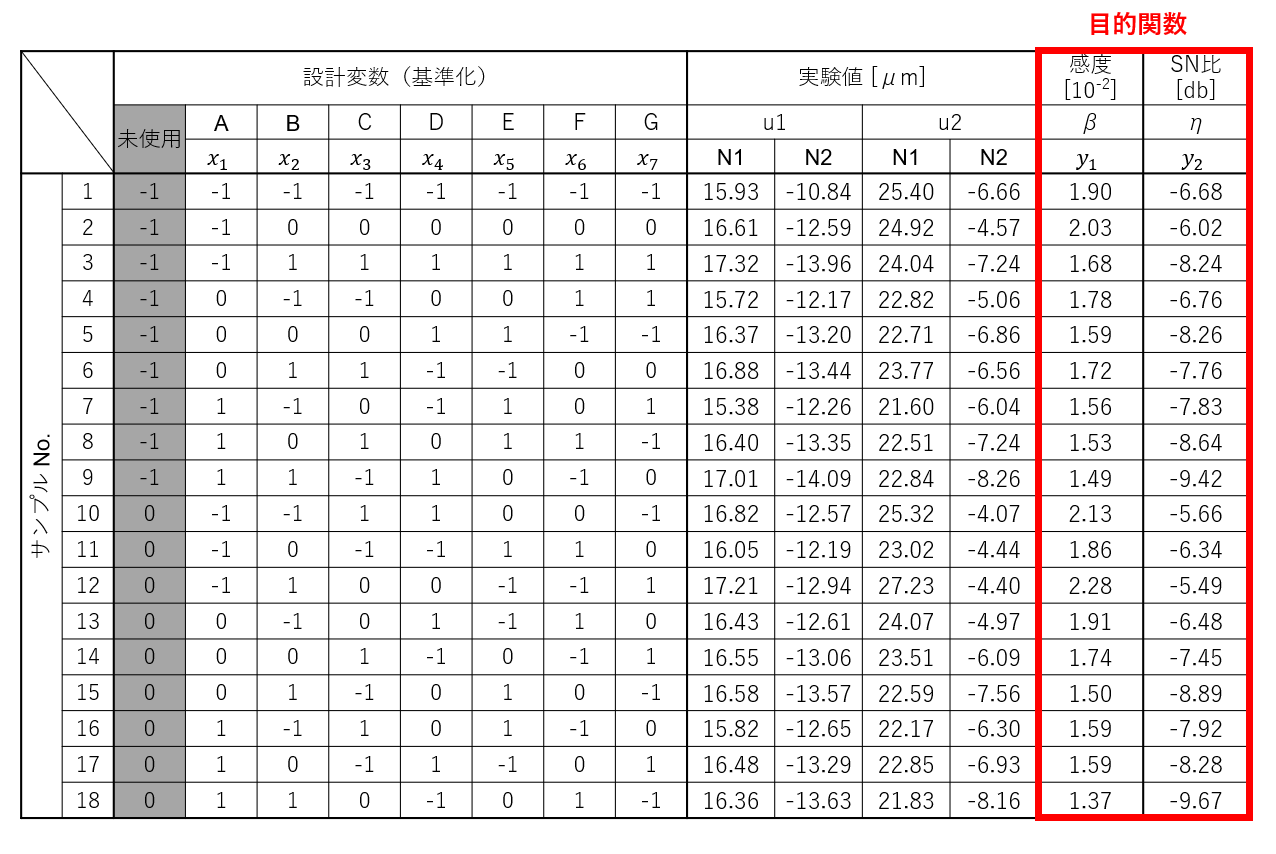
実験サンプル数は18なので、\(m=18\)、設計変数は7個なので\(n=7\)です。
なお、2つの目的関数の応答曲面を各々求めることになりますが、手順は全く同じです。そのため、以降では「感度」の場合についてのみ記載をします。
応答曲面関数の導出
応答曲面関数の導出のフローチャートを下に示します。
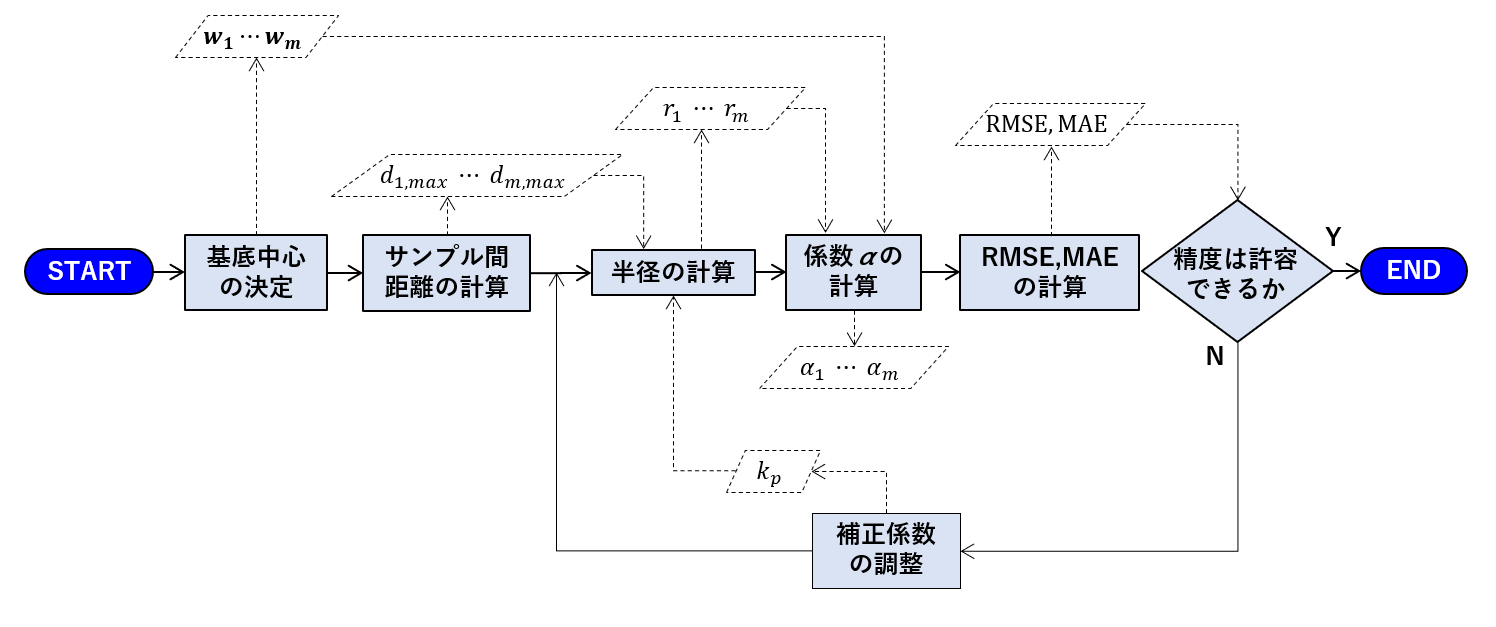
基底中心、半径、係数と順に求めていき、最後にフィッティング精度の確認を行います。フィッティング精度の結果によって、補正係数を調整し、再度計算を行います。
しかし、補正係数の調整を試行錯誤的に行うのは効率が良くありません。
そこで、基底中心の決定以後は、補正係数の値をある範囲で変化させて曲面フィッティングを行い、精度が最もよいときの補正係数値を採用することにします。補正係数の調整以外は、すべて自動で計算ができますので、プログラミングしてしまえば簡単に実行することができます。各々の計算式は前回記事を参照ください。
また、今回のフローチャートには含めていませんが、フィッティング精度の結果に応じて、追加実験を行うことも想定されます。RBFネットワークは、所望の精度が得られるまで逐次的にサンプル追加といったことができます。
基底中心の決定
最初に、基底中心\(\boldsymbol{w}_1 \cdots \boldsymbol{w}_m\)を決めます。
前回の記事で、基底中心は実験の際の設計変数の値とすることを述べました。すなわち、今回の場合、基底中心は直交表の行ということになります。
設計変数の値は、\(-1~1\)の範囲に基準化されたものを用います。

なお、基底中心は、感度とSN比の両方で同じものになります。
補正係数\(k_p\)を変化させたときのフィッティング精度
補正係数\(k_p\)を\(1~40\)の範囲の整数として、半径\(r_1 \cdots r_m\)および係数\({\alpha}_1 \cdots {\alpha}_m\)を計算し、フィッティング精度RMSE,MAEを計算しました。結果は次の通りです。
RMSE、MAEはそれぞれ、大域的フィッティング精度、局所的フィッティング精度の指標です。これらは、数値が低いほど精度が高い性質を持っています。今回の場合、両者とも\(k_p=4\)において最適となります。
このときのRMSEおよびMAEの数値は、次の通りです。
$$\begin{array}{lll}
{\rm{RMSE}}&=&8.06^{-5}\\
{\rm{MAE}}&=&1.70^{-4}\\
\end{array}$$
オーダーは十分に小さいので、フィッティング精度は許容できると判断しました。
\(k_p=4\)のときの係数\(\boldsymbol{{\alpha}}\)および、半径\(\boldsymbol{r}\)の値は次の通りです。
$$\boldsymbol{{\alpha}}=
\left[ \begin{array}{r} 6.43\times10^{-3} \\ -1.45\times10^{-2} \\ 2.92\times10^{-3} \\ -1.64\times10^{-3} \\ -7.09\times10^{-3} \\ -2.67\times10^{-3} \\
2.70\times10^{-3} \\ -1.19\times10^{-3} \\ 4.03\times10^{-4} \\ 1.54\times10^{-2} \\ 1.06\times10^{-2} \\ 2.29\times10^{-2} \\
2.52\times10^{-3} \\ -7.32\times10^{-3} \\ -1.58\times10^{-3} \\ 5.23\times10^{-3} \\ -3.12\times10^{-3} \\ 2.14\times10^{-4} \end{array} \right]$$
$$\boldsymbol{r}=
\left[ \begin{array}{r} 4.94 \\ 2.85 \\ 4.94 \\ 3.49 \\ 3.49 \\ 3.49 \\
3.77 \\ 3.77 \\ 3.77 \\ 3.77 \\ 3.77 \\ 3.77 \\
3.49 \\ 3.49 \\ 3.49 \\ 3.77 \\ 3.77 \\ 3.77 \\ \end{array} \right]$$
これで、RBFネットワークのすべてのパラメータ(基底中心、半径、係数)が求まりました。
応答曲面形状の確認
応答曲面の形状を実際に確認します。しかし、設計変数は7個なので、応答曲面は8次元空間に浮かぶ7次元の超平面です。もはや、図示もイメージもできません。
そこで、7個の設計変数から2個を取り出し、その他の設計変数の数値を0に固定したときの曲面形状を見ていきます。7個から2個を取り出すので、その組み合わせは\({{}_7}C_2=21\)です。したがって、21枚のグラフが描けます。
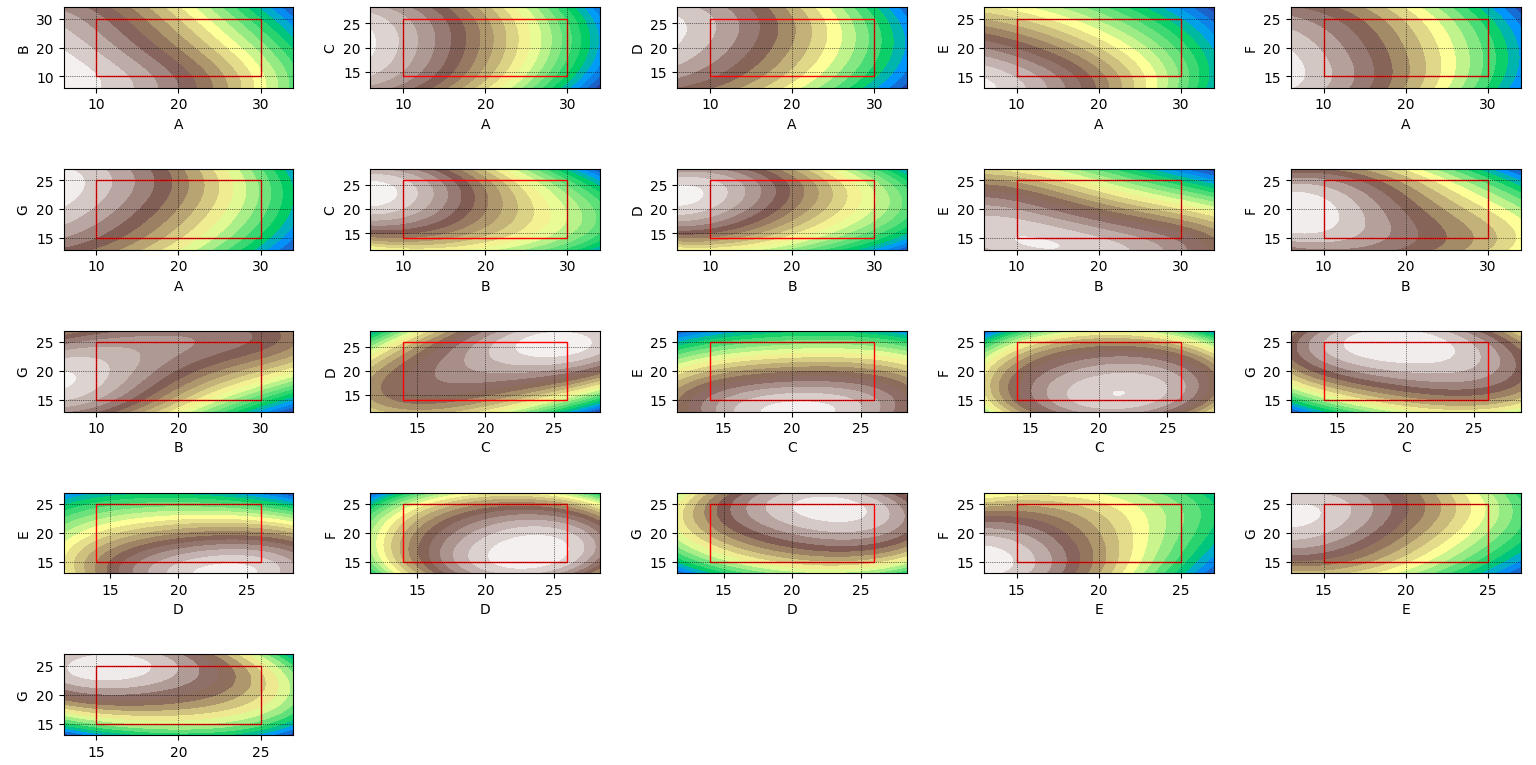
これらのグラフの見方は、地形図と同じで、青→緑→茶となるにつれ、数値が大きくなります。赤い四角は、実行可能領域を示します。
これだけの枚数があるとどこを見ればよいのか目移りしますが、ここでは、要因効果図の結果と相違ないかを確認することにします。
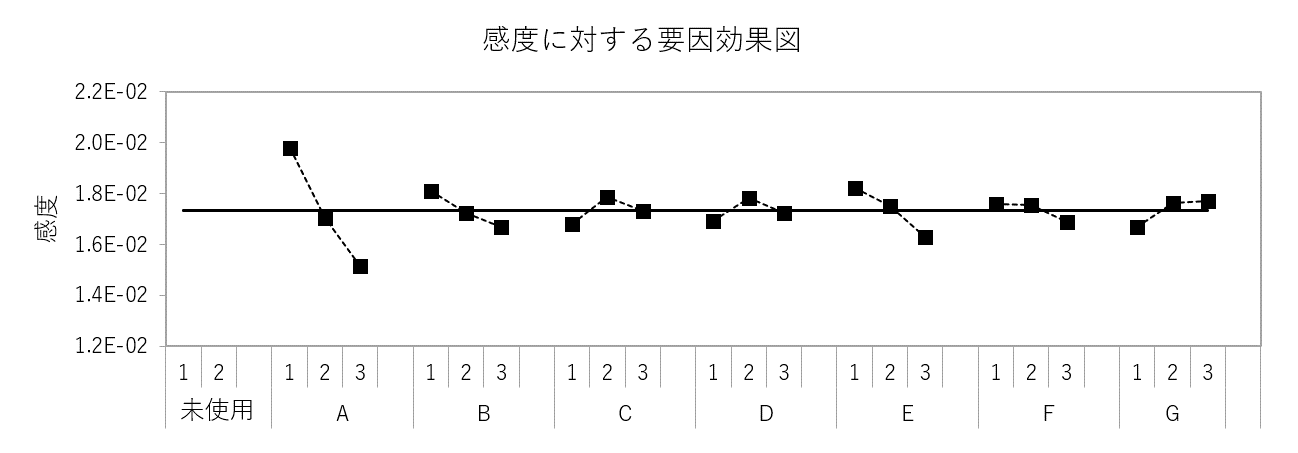
例えば、Aについて確認する場合、まず、応答曲面グラフの中でAの軸に注目します(6個あります)。
それらの軸を観察すると、Aの値が大きいほど、関数値(感度)が小さくなることが読み取れます。このことは、要因効果図と一致します。
同じように、他の設計変数についても見て行くと、応答曲面プロットと要因効果図とで傾向が一致することが分かります。したがって、ある程度は応答曲面関数は適切であると判断することができます。
その他にも、可能であれば、曲面フィッティングに用いたサンプルとは異なる水準の追加サンプルで実験を行い、結果を応答曲面関数の値と比較するといった確認方法も有効です。
ここまでで、感度に関する応答曲面関数が求まりました。上述の通り、ここまでの作業をSN比についても実施し、SN比に関する応答曲面関数を求めます(詳細省略)。
この2つが多目的最適化問題における目的関数になります。
まとめ
多目的最適化問題を解く前段取りとしての、RBFネットワークによる応答曲面法について説明しました。今回は、前回説明したことの実践として、デモ問題の設計対象について、実験データから応答曲面関数を実際に求める作業を追っていきました。
ここまでのことは、多目的最適化問題を解くための準備といった位置づけになります。次回からは、今回求めた2つの目的関数について、実際にパレートフロントを求める作業について説明をします。