多目的最適化問題(第二回)
RBFネットワークによる応答曲面法(前半)
本記事は、多目的最適化問題についての第二回になります。前回示したフローチャートで下の赤枠内の内容になります。
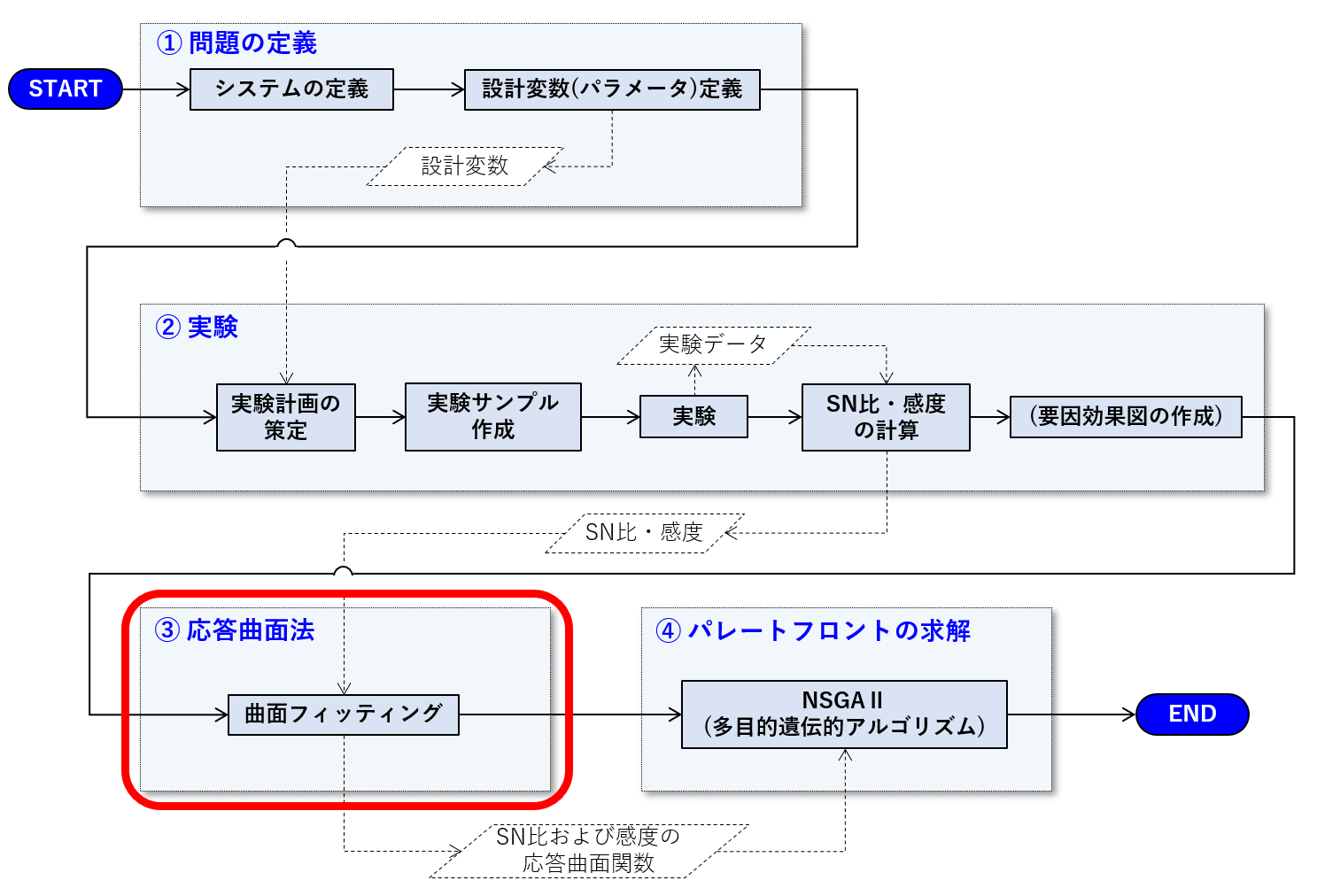
今回の内容は、直接的に多目的最適化問題に関わるわけではありません。実験(シミュレーション)でしか目的関数の値が得られない設計対象について最適化問題を解くために、必要なステップです。
多目的最適化に限らず、多くの最適化問題では、解を得るアルゴリズムの中で反復計算を行います。したがって、数式が分かっていないと解を得ることは困難です。
設計実務で扱うような対象の場合、”その数式が分かっていない”、あるいは、”複雑で導出困難な場合”が多いです。そのような場合、何らかの関数で設計対象を近似化することが行われます。近似の技法として、実験データを用いる応答曲面法が有効です。
応答曲面法については、別記事で説明をしています。今回はこのときとは異なる手法で応答曲面を求めることが求められます(理由後述)。
応答曲面法に用いる関数について
2次関数による目的関数の近似については別記事にて説明しています。
大まかに説明すると、Box-Benhken計画に基づき、実験(シミュレーション)データを収集し、最小二乗法で曲面フィッティングを行いました。
今回も同じ方法で進められれば良いのですが、そうは行きません。なぜならば、最小二乗法では少なくとも未知数の数以上のデータが必要になるのですが、今回はデータ数がそれに満たないからです。
ここでいう未知数とは、2次関数の各項の係数と切片です。本設計対象では、係数は36個です。一方、ロバストパラメータ設計で用いた実験計画では18個のデータしかありません。
新たにデータを加えるのも良いのですが、手間がかかります。ここでは、2次関数ではなく、別の関数を用いることでこの問題を回避しようと思います。
RBFネットワーク
応答曲面法では、2次関数の他に「RBFネットワーク」と呼ばれる関数が良く用いられます。RBFネットワークとは、次式で表される関数です。
$$y=f(\boldsymbol{x})=\sum_{j=1}^{m}{{\alpha}_j \cdot K(\boldsymbol{x}, \boldsymbol{w}_j)}$$
\(\boldsymbol{x}\)は、関数の入力で設計変数です。
$$\boldsymbol{x}=\begin{bmatrix}
x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}$$
\(n\)は設計変数の個数です。
\(K(\boldsymbol{x}, \boldsymbol{w}_j)\)は、基底関数と呼ばれる非線形関数で、\(\boldsymbol{w}_j\)は基底中心と呼ばれ、設計変数と同次元のベクトルです。また、\({\alpha}_j\)は係数です。
RBFネットワークをは、図で示すと以下のようになります。
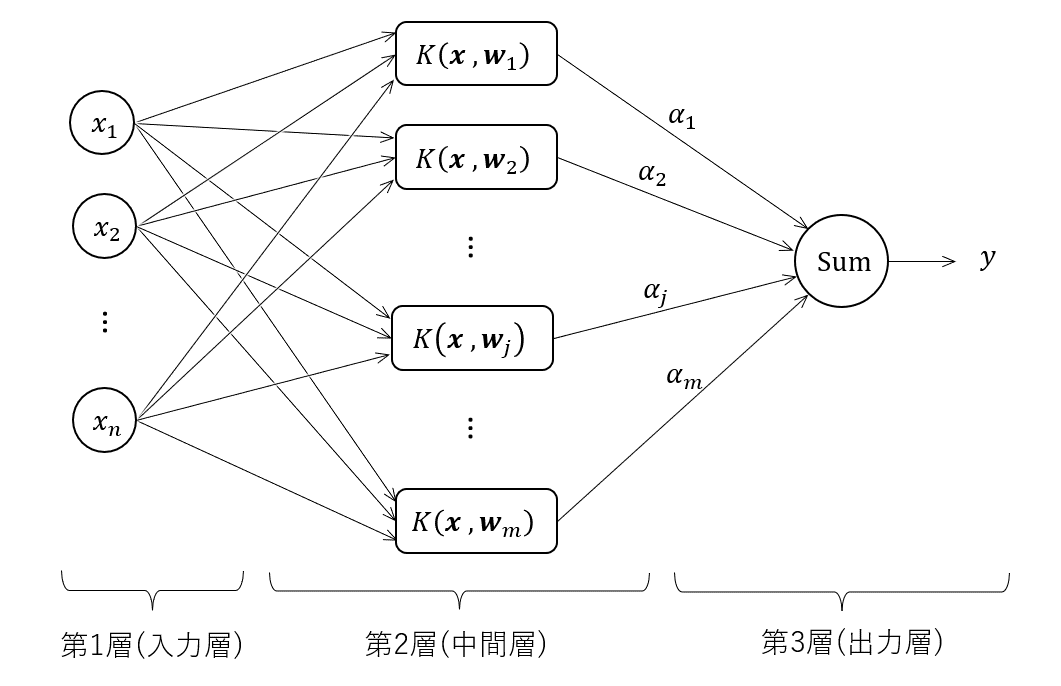
このように、RBFネットワークは、3層からなるニューラルネットワークの一種です。
- 第1層(入力層): 関数の入力変数(この場合、設計変数)
- 第2層(中間層): \(m\)個の非線形関数ユニット
- 第3層(出力層): 中間層の各出力に係数\({\alpha}_1 \cdots {\alpha}_m \)を乗じて和を取る
このニューラルネットワークの性質は、中間層の非線形関数によって決まります。
動径基底関数
RBFネットワークの中間層の非線形関数\(K(\boldsymbol{x}, \boldsymbol{w}_j)\)は、具体的には次式です。
$$K(\boldsymbol{x}, \boldsymbol{w}_j) = {\rm{exp}}\left\{ \frac{(\boldsymbol{x}-\boldsymbol{w}_j)^T(\boldsymbol{x}-\boldsymbol{w}_j)}{{r_j}^2}\right\}$$
これは、動径基底関数(Radial Basis Function)と呼ばれます。この頭文字を取って、RBFというわけです。
\(\rm{exp}\)は指数関数です。また、\(r_j\)は、半径と呼ばれるパラメータです。
動径基底関数の特徴
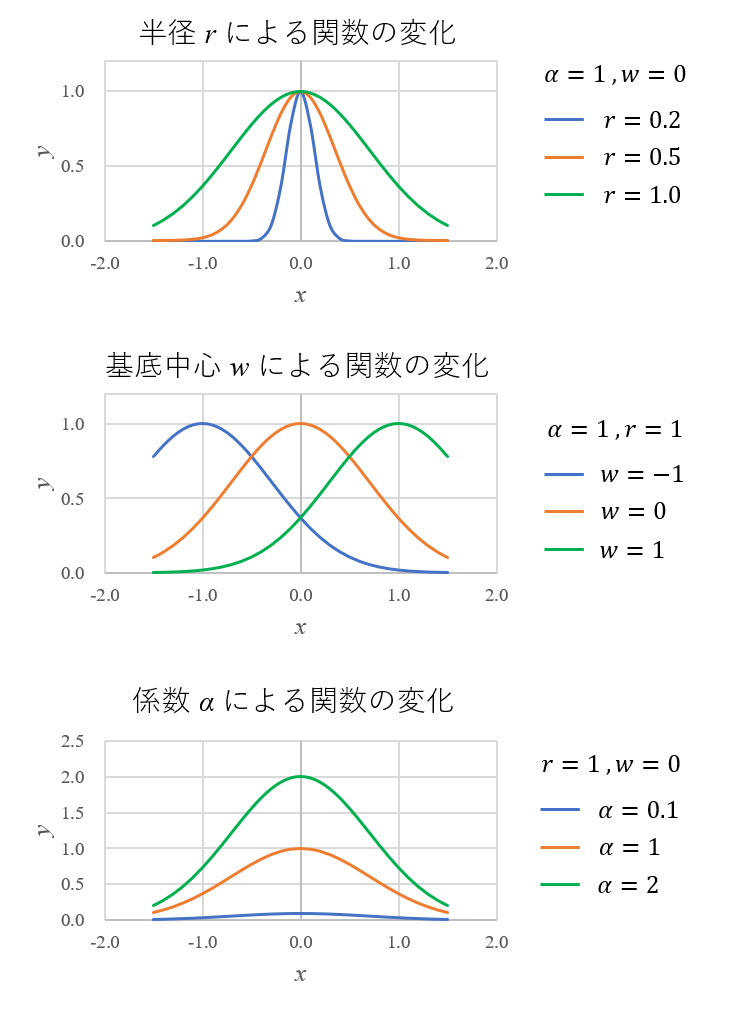
動径基底関数はどのような関数なのか、1入力の場合について係数も含めて見ていきます。この場合の関数式は、次の通りです。
$$y=\alpha \cdot {\rm{exp}}\left\{ \frac{(x-w)^2}{{r}^2}\right\}$$
\(r\)、\(w\)、\(\alpha\)をそれぞれ変化させたときの関数の出力をプロットしたものを以下に示します。
これらのプロットから次のことが分かります。
- 動径基底関数は、基底中心\(w\)を中心に対称形である。
- 半径値\(r\)が小さいと、関数形状は急峻になり、大きくするとなだらかになる。
- 係数値\(\alpha\)が大きいと関数形状が全体的に大きくなる。
入力数(設計変数の数)が多くなると、関数の形状は図示できなくなりますが、1入力のときの特徴を押さえておけば何となくイメージできると思います。
RBFネットワークによる曲面フィッティング
RBFネットワークによる曲面フィッティングでは、「基底中心」「半径」「係数」の3つを決める必要があります。
基底中心 \(\boldsymbol{w}_1,{\cdots},\boldsymbol{w}_j,{\cdots},\boldsymbol{w}_m\) の決め方
基底中心\(\boldsymbol{w}_1,{\cdots},\boldsymbol{w}_j,{\cdots},\boldsymbol{w}_m\)は、通常、実験データを取得したときの設計変数値を用います。つまり、中間層のユニット数\(m\)は、実験データの数と同じになります。
半径 \(r_1,{\cdots},r_j,{\cdots},r_m\) の決め方
次に半径 \(r_1,{\cdots},r_j,{\cdots},r_m\)ですが、RBFネットワークによる応答曲面法では、これが調整パラメータになります。逆に言えば、明確な決め方はありません。
次のような式を用いて\(r_j\)を決める方法などがありますが、あくまでも経験に基づくものです。
$$r_j = \frac{d_{j,max}}{\sqrt{n}\sqrt[n]{m-1}}$$
\(d_{j,max}\)は、\(j\)番目の実験サンプルにおける設計変数ベクトルを基準にして、ほかの実験サンプルでの設計変数との"距離"の最大値です。
$$d_{j,max}={\rm{max}} \left\{ \sqrt{(\boldsymbol{w}_j-\boldsymbol{w}_{other})^T(\boldsymbol{w}_j-\boldsymbol{w}_{other})} \right\}$$
\(\boldsymbol{w}_{other}\)は、\(j\)番目の実験サンプル\(\boldsymbol{w}_j\)以外の実験サンプルを意味します。
私は、上式によって一旦\(r_j\)を算出して曲面フィッティングを行い、目的関数の推定値と実験値を比較し、必要に応じて係数をかけて補正することを良く行っています。すなわち、補正係数を\(k_p\)とすると、
$$r_j = k_p \cdot \frac{d_{j,max}}{\sqrt{n}\sqrt[n]{m-1}}$$
です。
係数 \({\alpha}_1,{\cdots},{\alpha}_j,{\cdots},{\alpha}_m\) の決め方
係数\({\alpha}_1,{\cdots},{\alpha}_j,{\cdots},{\alpha}_m\)は、以下に記す手順で計算されます。なお、ここでは手順のみの説明とし、この手順の導出については説明を省略します。
まず、実験データ収集時の設計変数値(=基底中心)を用いて、次のような行列を作ります。
$$\boldsymbol{K}=
\begin{bmatrix}
K(\boldsymbol{w}_1, \boldsymbol{w}_1) & K(\boldsymbol{w}_1, \boldsymbol{w}_2) & \cdots & K(\boldsymbol{w}_1, \boldsymbol{w}_m)\\
K(\boldsymbol{w}_2, \boldsymbol{w}_1) & K(\boldsymbol{w}_2, \boldsymbol{w}_2) & \cdots & K(\boldsymbol{w}_2, \boldsymbol{w}_m)\\
\vdots & \vdots & \ddots & \vdots \\
K(\boldsymbol{w}_m, \boldsymbol{w}_1) & K(\boldsymbol{w}_m, \boldsymbol{w}_2) & \cdots & K(\boldsymbol{w}_m, \boldsymbol{w}_m)\\
\end{bmatrix} $$
\(\boldsymbol{\alpha}=[{\alpha}_1,{\cdots},{\alpha}_j,{\cdots},{\alpha}_m]^T\)とすると、\(\boldsymbol{\alpha}\)は、
$$\boldsymbol{\alpha}=(\boldsymbol{K}^T\boldsymbol{K}+\boldsymbol{\Lambda})^{-1}\boldsymbol{K}^T\boldsymbol{y}$$
で計算されます。
\(\boldsymbol{y}\)は実験データを格納した列ベクトルで、\(\boldsymbol{\Lambda}\)は次に示す\(m{\times}m\)の行列です。
$$\boldsymbol{\Lambda}=\begin{bmatrix}
\gamma & 0 & \cdots & 0 \\
0 &\gamma & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \gamma \\ \end{bmatrix} $$
\(\boldsymbol{\Lambda}\)は逆行列の存在を保証するためのもので、通常は、\(\gamma=0.01\) 程度の数値となります。
逐次的運用と曲面フィッティング精度
RBFネットワークの中間層のユニット数は実験サンプルの数と等しいと先に述べました。ということは、曲面フィッティングの精度を確認しながら逐次的に実験データを追加することが可能です。実験にかかるコストが大きい場合に有用な特徴になります。そして、これは機械学習の特徴の1つでもあります。
以下、曲面フィッティングの精度の確認について、説明をします。曲面フィッティング精度には2種類の指標があります。
大域的フィッティング精度
大域的フィッティング精度とは、「実行可能領域の全体に渡って曲面(応答曲面関数の出力値)が実験結果とマッチしているのか」を意味します。
二乗平均平方根誤差(RMSE: Root Mean Squared Error)と呼ばれる指標で計ることができます。
$${\rm{RMSE}}=\sqrt{\frac{\sum^{m}_{j=1}{(y_j-\hat{y}_j)^2}}{m}}$$
\(y_j\)は\(j\)番目の実験データで、\(\hat{y}_j\)は応答曲面関数の\(j\)番目の出力値です。
局所的フィッティング精度
大域的と対照的な概念に”局所的”があります。実行可能領域のある1点におけるフィッティング精度が「局所的フィッティング精度」です。これは、最大絶対値誤差(MAE: Maximum Absolute Error)で計ることができます。
$${\rm{MAE}}={\rm{max}}\left| y_j-\hat{y}_j \right|$$
まとめ
RBFネットワークによる応答曲面法について説明をしました。
RBFネットワークとは動径基底関数を用いたニューラルネットワークの一種です。機械学習と同じような運用が可能で、曲面フィッティングの精度を確認しながら、逐次的に実験データの追加といった作業ができます。
今回は数式ばかりになってしまいましたが、次回でデモ問題の設計対象について実際にRBFネットワークでの応答曲面法の適用してみます。