材料力学の基礎

はじめに

本記事では、機械設計で重要な4力学の1つである「材料力学」の基本について解説します。
材料力学の目的は、材料の破壊や降伏の有無を考える分野です。
初回は、基本中の基本である「応力とひずみ」を説明します。

近年は、3D-CAD、CAEが普及し、機械設計に活用されています。モデリングと条件設定してやれば、"応力"は簡単にシミュレーションができます。

しかし、シミュレーションは「答え」ではありません。機械設計者の仕事の1つは、シミュレーション結果の解釈と考察です。そのためには、正しい知識が必要です。

引っ張られる棒

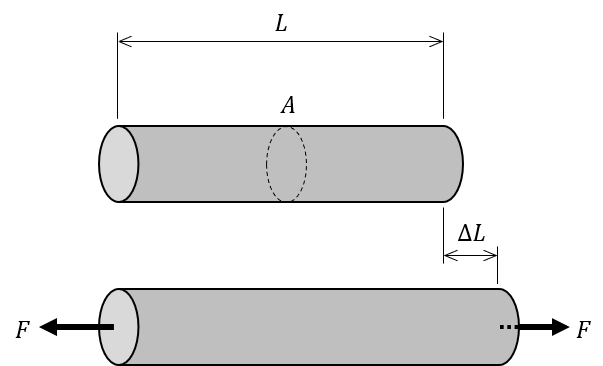
おそらく、材料力学の参考書などで最初に出てくるのは、次のような図です。
これをベースに考えてみます。

応力とひずみの"数式"

上の図は、長さ\(L\)で断面積\(A\)の棒に、軸方向に外力\(F\)を加えて引っ張ると\({\Delta}L\)だけ伸びた状態を表しています。(厳密には、引っ張られると断面積は減少するのですが、今は無視します)

このとき、応力\(\sigma\)は、

$$\sigma=\frac{F}{A}\tag{1}$$

で、ひずみ\(\epsilon\)は、

$$\epsilon=\frac{{\Delta}L}{L}\tag{2}$$

です。

また、応力とひずみは比例関係にあり、

$$\sigma=E\epsilon\tag{3}$$

という式で結びつきます。この比例係数\(E\)を縦弾性係数(ヤング率)と言います。

多くの方はこのように覚えているのではないでしょうか。実際にこのように説明している書籍も存在しています。では、これらの式の意味するところを正確に説明できますか。

応力の意味

応力とは棒の内部で発生している外力と釣り合う力です。応力は単位面積当たりの大きさで表されます。これを表しているのが、式\((1)\)です。式\((1)\)を変形すると、\({\sigma}A=F\)であり、右辺の外力と左辺の応力が釣り合っていることを意味しています。

ひずみの意味

ひずみは、式\((2)\)のとおり、物体の元の大きさと変形量の比です。分母と分子が同じ単位なので、無次元量です。
同じ外力を加えても、物体の大きさによって変形絶対量が違うので、このような量で物体の変形の度合いが表されています。

縦弾性係数の意味

応力とひずみが比例関係にあることは、経験的に古くから分かっていました。また、実験によって、その比例係数が「材料によって固有の数値になること」も分かっていました。
この材料固有の比例係数が縦弾性係数です。応力とひずみを結び付けている量で、物体の変形のしにくさ(剛性)を意味します。

結言

最初に述べたように、今はCAEソフトウェアを使えば簡単に応力シミュレーションができます。
部材の応力分布や最大の応力の値が簡単に視覚化できて便利です。

以前、メーカに勤めていたとき、私も3D-CADと構造解析ソフトウェアを使ってシミュレーションをしていました。
とある同僚が、「最大応力値が許容値を超えた」というので、「材料の種類を変えて」何度もシミュレーションしていました。しかし、何度やっても結果が変わらず、その同僚は頭を抱えていました。それも当然で、材料を変えることによって変わるのは縦弾性係数だけだからです。

前述の通り、「応力とは物体の内部で発生する、外力と釣り合う力」なのだと理解していれば、同僚の発想は正しくないと分かります。この式\((1)\)には、縦弾性係数\(E\)の情報は一切入っていません。

同僚の頭の中には、\(\sigma=E\epsilon\)の式しかなかったのです。

応力、ひずみ、縦弾性係数は、材料力学の基本中の基本です。しかし、その意味を理解していないと、思わぬところで足をすくわれます。材料力学に限ったことではありませんが。

※厳密には、変形後の形状が材料の剛性(縦弾性係数)によって変わるので、最大応力値は全く変わらないわけではない。