応答曲面法による最適化設計(第二回)
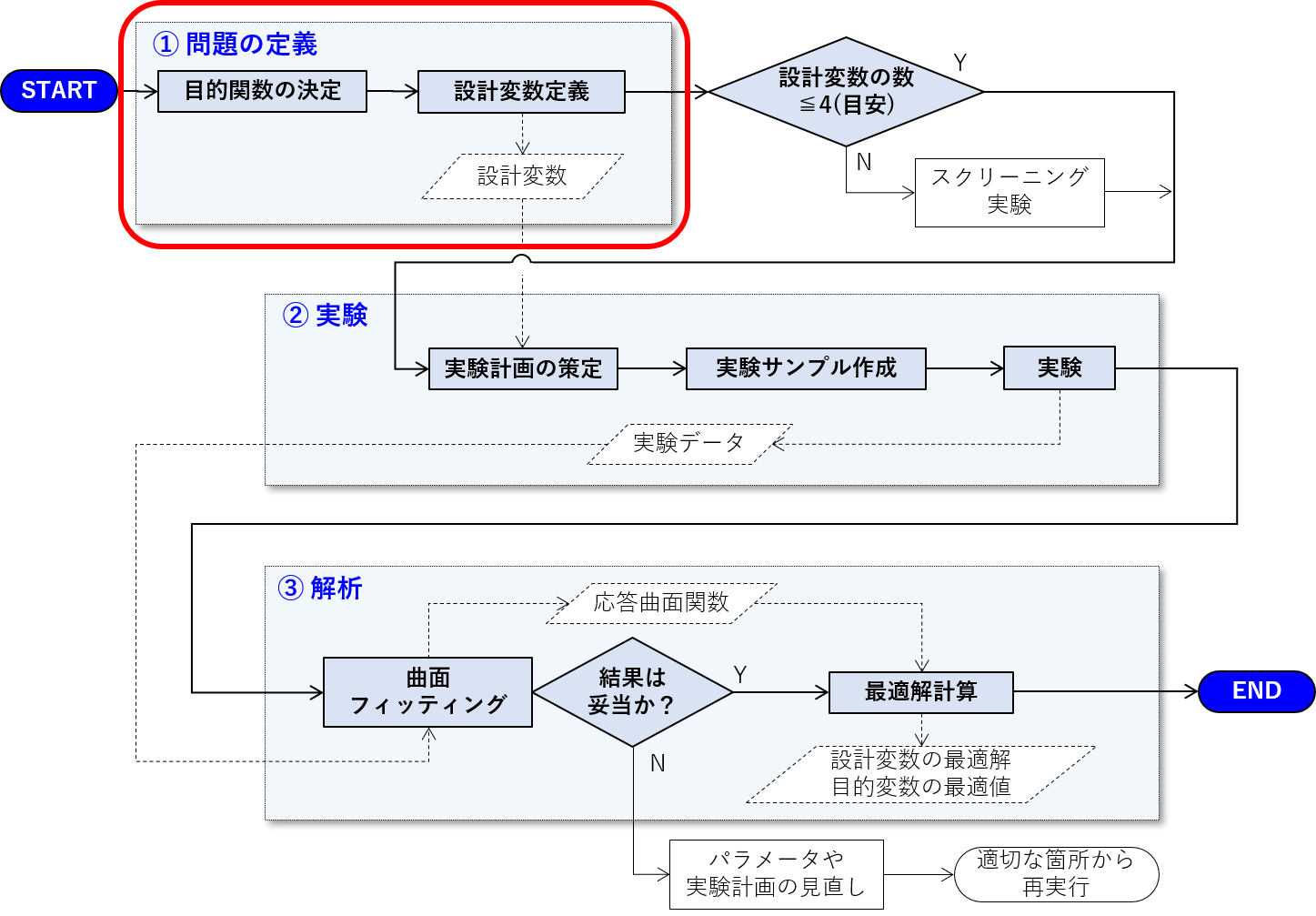
問題の定義
応答曲面法の第二回の記事になります。前回は、概要と設計対象について述べましたが、今回から本格的に設計を進めていきます。
本記事では下記に示す「問題の定義」について説明をします。
問題の定式化
応答曲面法では、実験データから曲面フィッティングすることは前回述べました。
この曲面は応答曲面と呼ばれます。最適化したい"量"はこの応答曲面に乗ることになります。
応答曲面は何らかの数式(関数)で表されます。どのような関数を用いるかによって応答曲面法はさまざまなバリエーションが存在します(詳しくは次回以降の、「曲面フィッティング」の記事にて説明)。
とりあえず、この段階では次式のように表します。
$$y=f(x_1,x_2,\cdots,x_n)$$
左辺\(y\)は、最適化したい量です。
一方、右辺は関数です。変数\(x_1,x_2,\cdots,x_n\)によって、数値が決まります。
この関数\(f(x_1,x_2,\cdots,x_n)\)を「目的関数」と呼び、変数\(x_1,x_2,\cdots,x_n\)を「設計変数」と呼びます。
目的関数と設計変数の定義
応答曲面法に限らず、最適化問題では最初に目的関数と設計変数を定義します。
目的関数
目的関数とは、最適化したい量のことであると先に述べました。
今回の設計対象であるモデルロケットでは、その飛翔性能のことですが、飛翔性能といっても様々あります。今回は、実際のモデルロケット競技でも種目として存在する「最高高度」を目的関数とします。
すなわち、目的関数の最適化とはこの場合、「最高高度の最大化」です。要するに、ロケットをより高く飛ばすことが目的です。
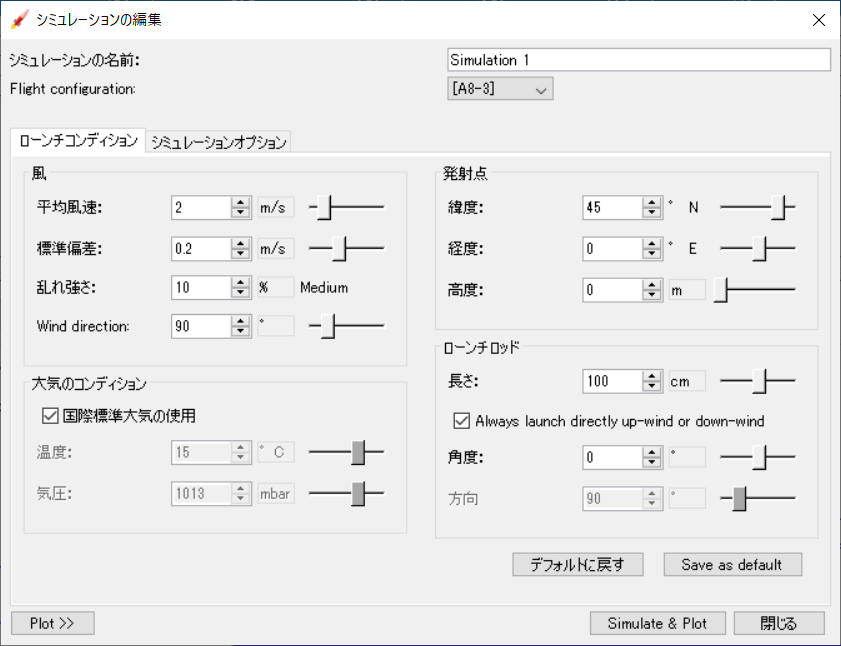
とりあえず、サンプルファイルのA simple model rocketでシミュレーションをしてみます。風などの条件は以下の通りです。
なお、今後実施するすべてのシミュレーションの条件は、これと同一とします。
サンプルファイルのシミュレーション結果は以下の通りです。
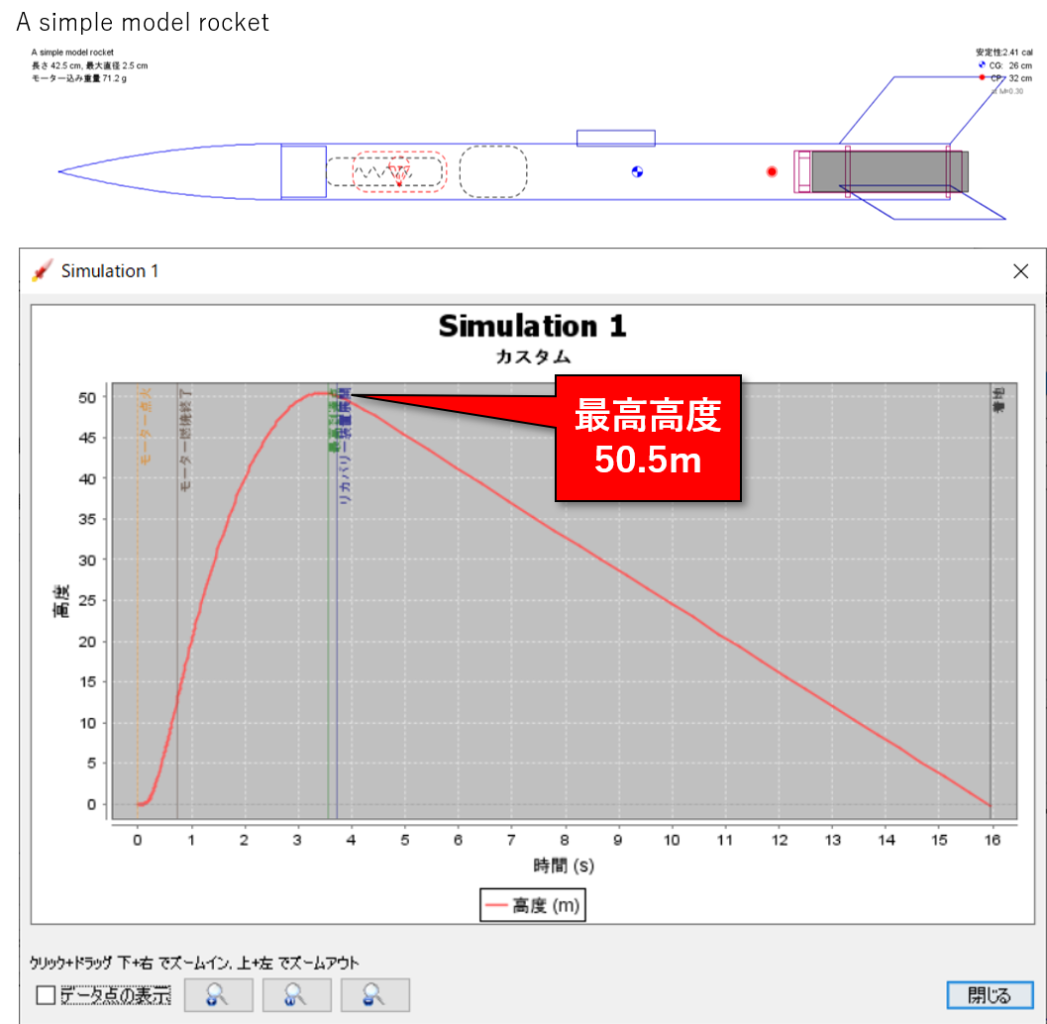
最高高度は50.5メートルです。また、風の条件に確率変数が含まれているので、試行によってばらつきがあります。ばらつきは±0.1m程度でした。
設計変数
次に設計変数を定義します。
設計変数は、最適化を目指して調整するパラメータです。
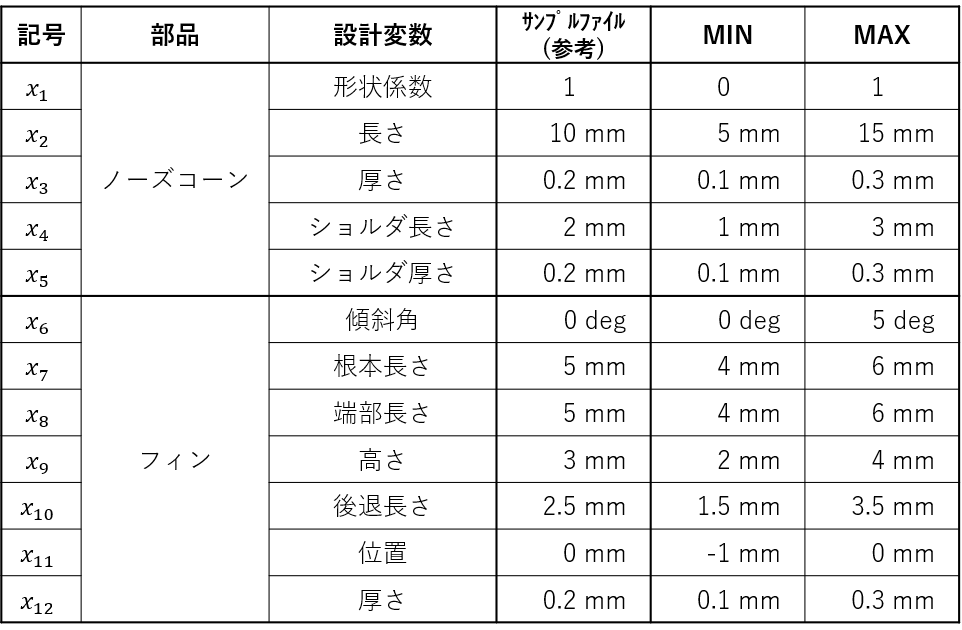
今回の場合、ノーズコーンとフィンの形状などを決定するパラメータです。材質やフィン枚数なども変更できますが、今回は"形状"のみに焦点を絞ることにします。調整できるパラメータを以下に列記します。
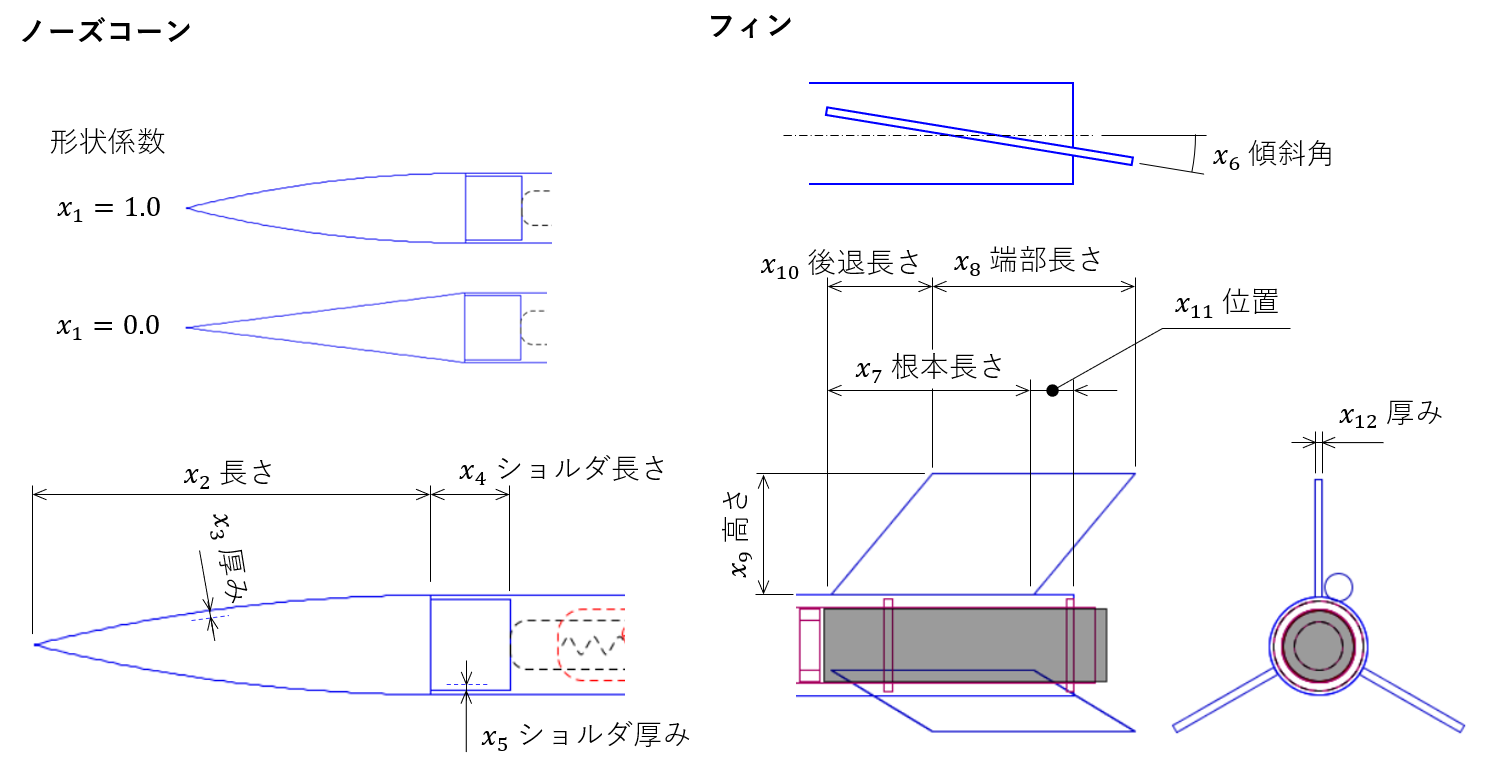
これらが設計変数になるわけですが、数値の範囲についても定義を行います。今回は、サンプルファイルの値を参考にして、適当な値を設定しました。
まとめ
応答曲面法による最適化設計を実施するにあたり、問題の定義について説明をしました。目的関数と説明変数の定義を行い、説明変数については数値範囲を決定しました。
次回は、「スクリーニング実験」について説明を行います。