応答曲面法による最適化設計（第三回）
スクリーニング実験

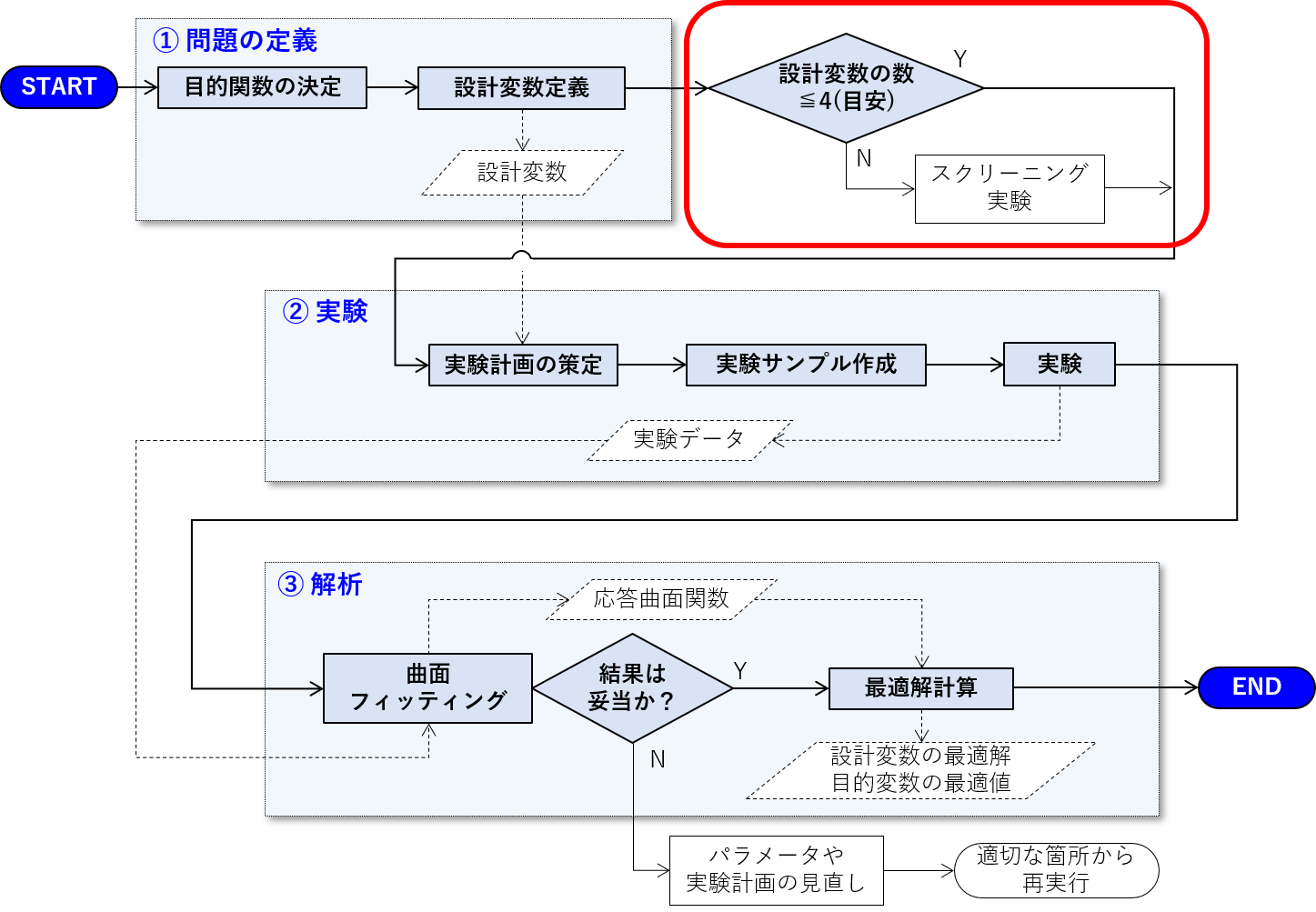
応答曲面法による最適化設計の第3回の本記事は、「スクリーニング実験」について説明をします。フローでは以下の位置になり、必要に応じて実施をする箇所になります。

スクリーニングとは

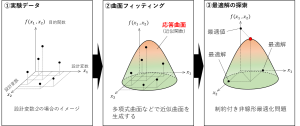
応答曲面法のイメージ図をご覧ください。下図は、設計変数は2つの場合について描いたものです。

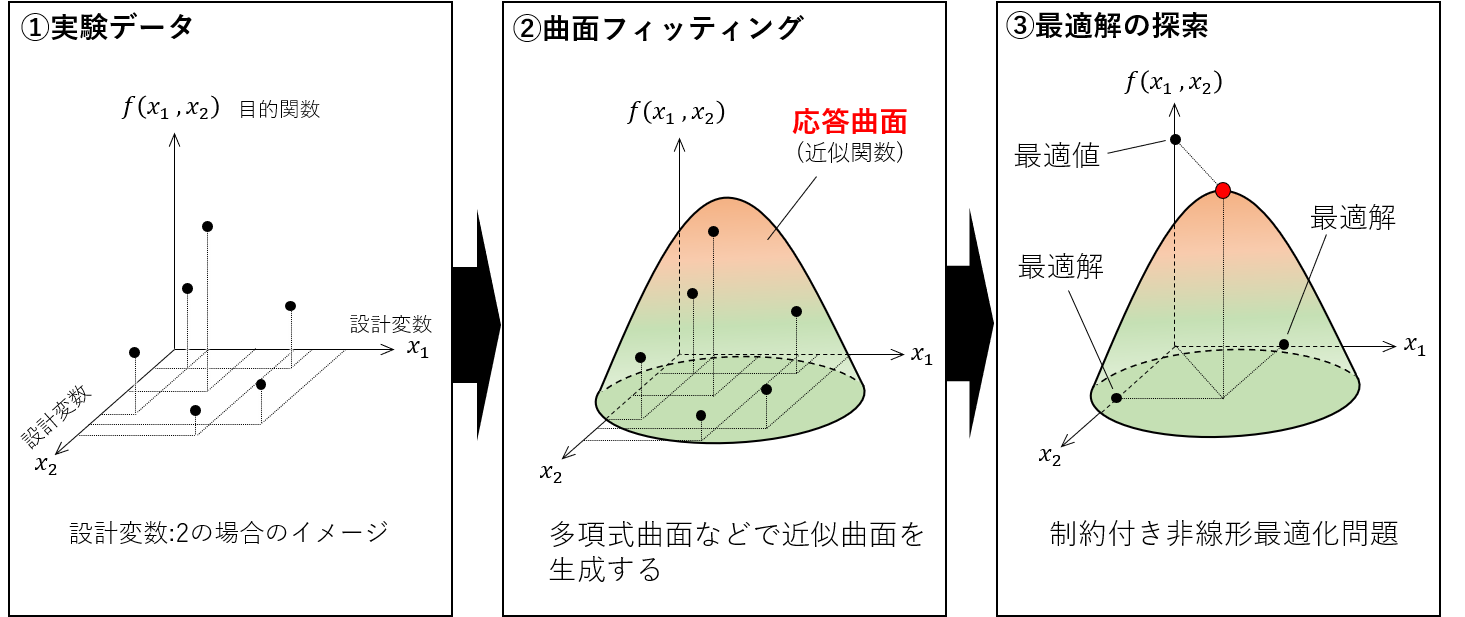
設計変数が2つなので、2次元平面にプロットできます（図の底面）。そして、その2次元平面に垂直な方向に目的関数の値（実験データ）の軸が配置されます。この実験データにフィットする曲面を生成するのが、応答曲面法です。つまり、この場合、応答曲面は3次元空間内の曲面です。

しかし、設計変数の数が2より多い場合はどうなるでしょうか。
応答曲面が存在する空間は4次元以上になります。並の人間には知覚できません。計算結果は出力されますが、図示できないため、結果解釈の難易度が跳ね上がります。

このように、設計変数の数が多いほど、結果の解釈の難易度が上がるのです。したがって、曲面フィッティングの対象にする設計変数の数は少ないほど望ましいのです。

そこで、結果に与える影響の大きい設計変数のみに絞り込んで曲面フィッティングを行う戦略が考えられます。この絞り込みを「スクリーニング」とも言います。

今回のデモ問題では、設計変数が12個です。経験上、設計変数の数は多くて4つ程度に抑えるのが良いです。したがって、今回は最初にスクリーニングを行うことにします。

スクリーニング実験

どのようにスクリーニングを行えばよいでしょうか。

同じようなことは、タグチメソッドのロバストパラメータ設計でも少し登場しています。
ロバストパラメータ設計では、直交表に基づく実験を行い、要因効果図から影響度の大きい設計変数を見定めていました。これと同様のことを行い、影響の大きい設計変数を抽出すればよいのです。これを「スクリーニング実験」と言います。

Plakett-Burman計画

ロバストパラメータ設計では、混合系直交表にて実験計画を作成しました。
今回は、影響の大きさだけ分かればよいので、もっと簡易な実験計画が望ましいと考えられます。

このような場合に用いられる実験計画として「Plakett-Burman計画」があります。Plakett-Burman計画は、2水準の実験計画で、Robin L.PlackettとJ.P.Burmanによって提案されました。主効果のみを検出し、実験数が少ないことが利点で、スクリーニングによく用いられます。

Plakett-Burman計画の実験数（サンプル数）は、設計変数の数よりも1以上大きい最小の4の倍数になります。今回のデモ問題では、サンプル数＝16です。

サンプル数16のPlakett-Burman計画の表を示します。見方は直交表と同じで、縦にサンプルNo.が並び、横に設計変数を割り付ける列が並びます。そして、表の要素は設計変数の水準を意味します。

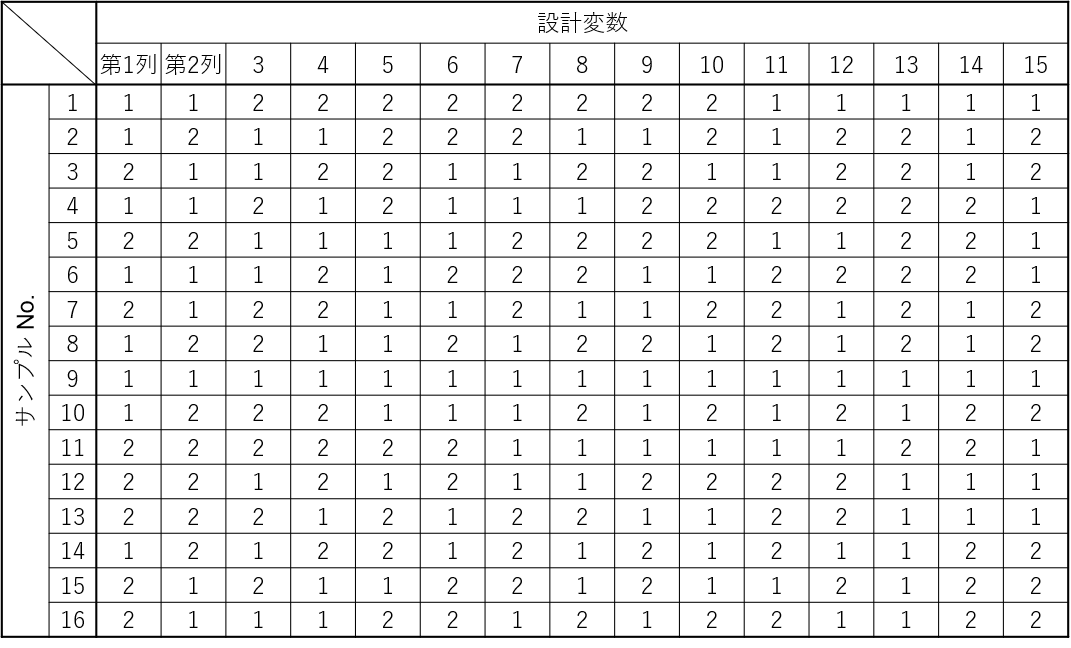
Plakett-Burman計画による実験計画の作成には、R（統計解析向けのプログラミング言語）のライブラリであるFrF2を使用しました。プログラミングは本記事のスコープ外なので詳細は記載しませんが、数理設計では必須のスキルです。RのほかにはPythonがよく使われます。

デモ問題のスクリーニング実験計画は以下のようになりました。設計変数は12個なのですべての列は使いません。

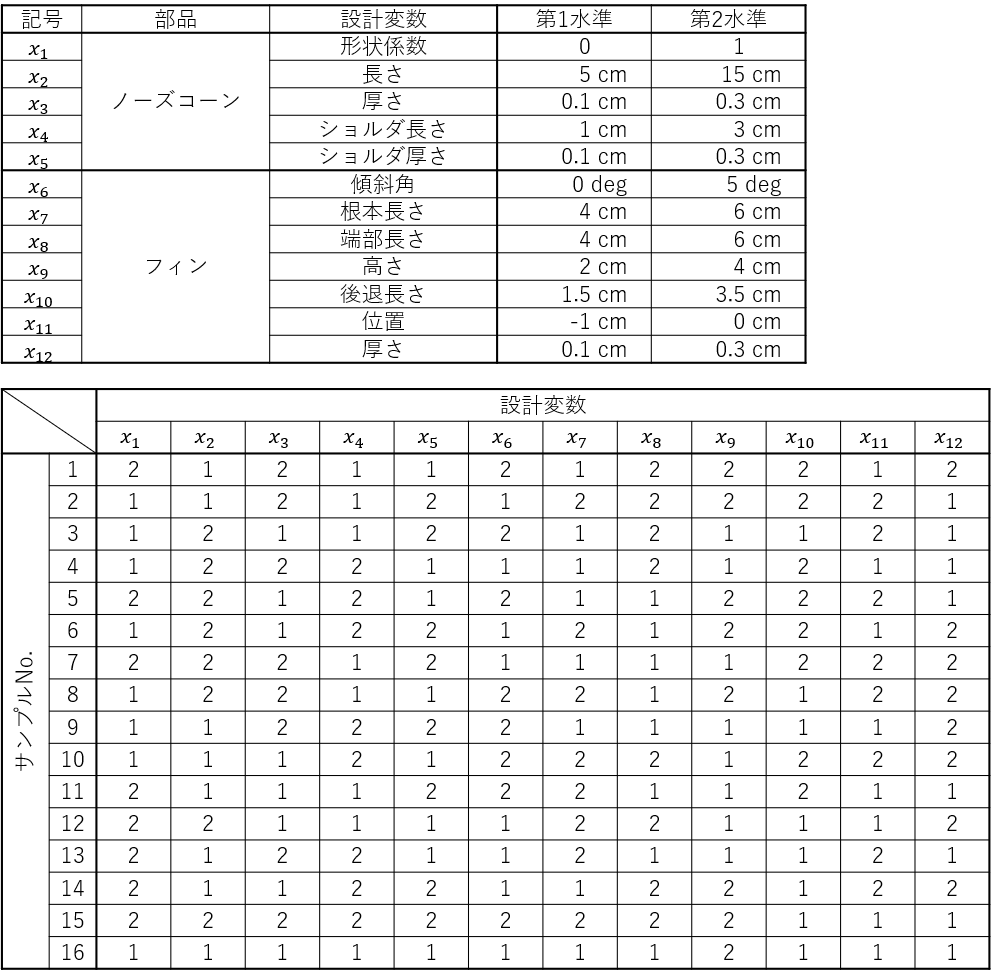
なお、水準の並びが先の表と違うのは、Rでの実験計画の生成の際に、実験順番のランダム化のオプションが入っていたためです。

実験結果

スクリーニング実験計画に基づき、OpenRocketでパラメータを調整して作成した16個のサンプルで飛翔シミュレーションを行いました。結果は以下の通りになりました。

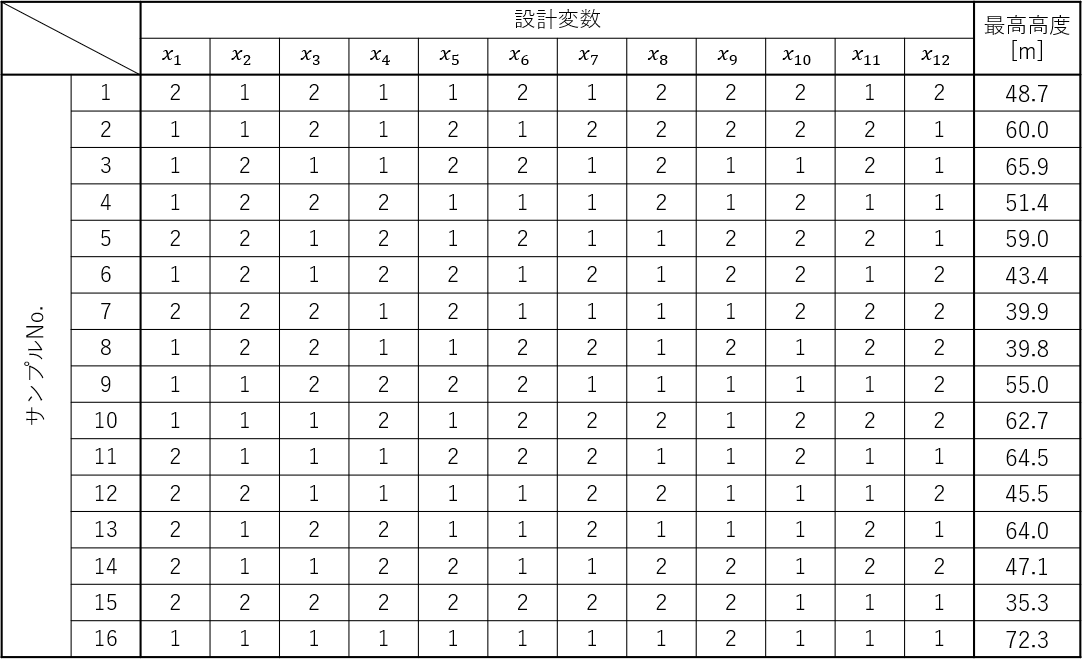
実験結果の分析

要因効果図の作成

実験データを対象に要因効果図を作成します。
手順はロバストパラメータ設計でやったときと全く同じです。各設計変数の各水準平均値を計算すればよいのでした。

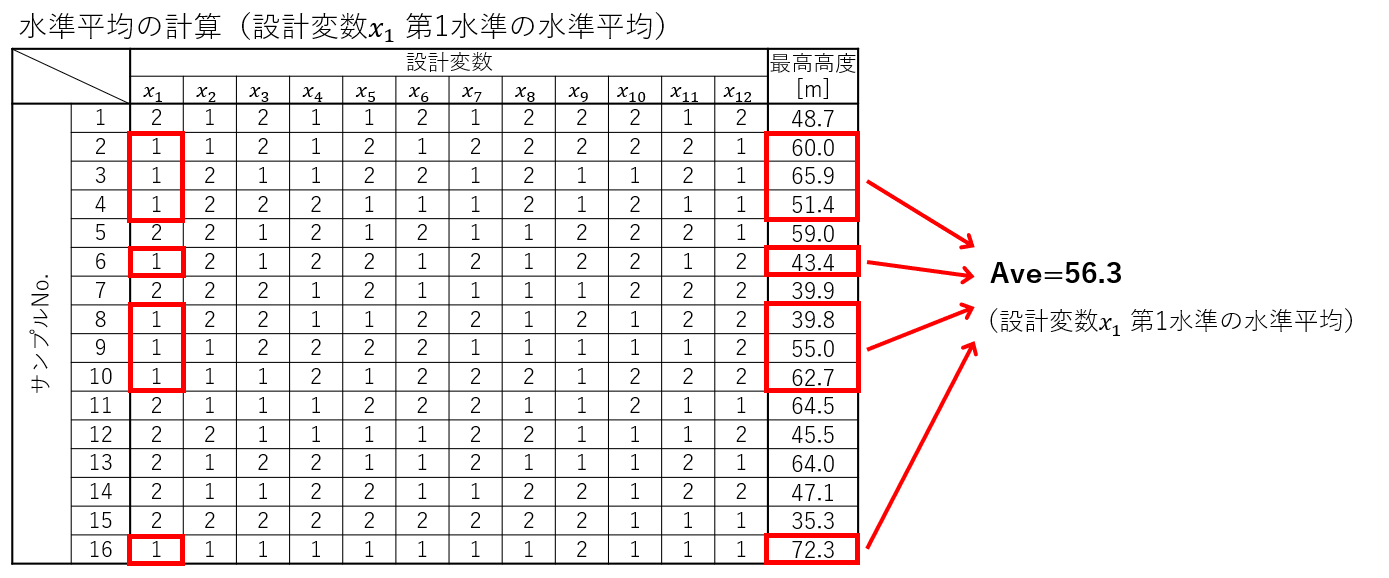
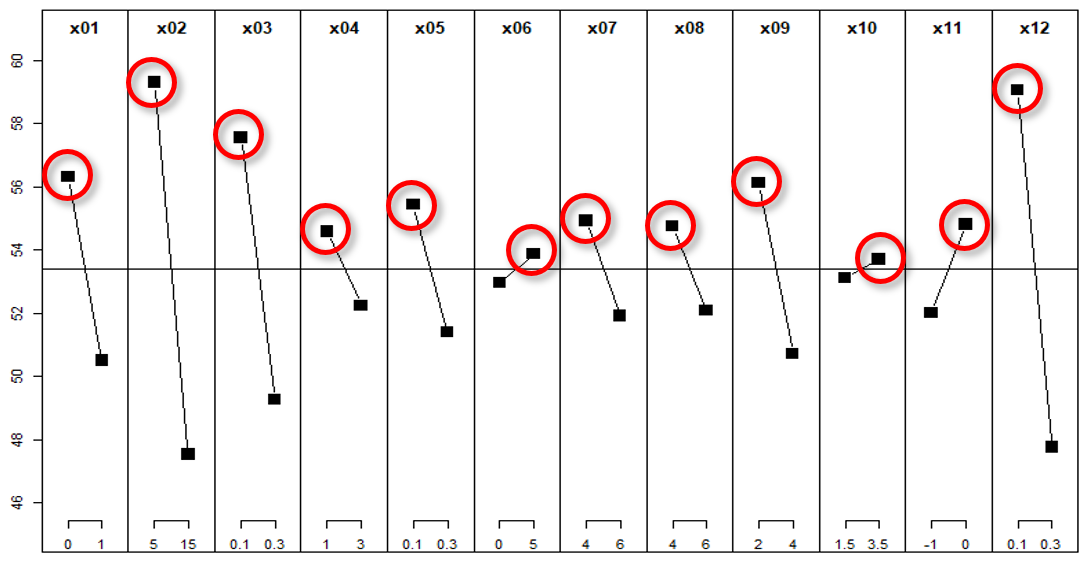
要因効果図は次のようになりました。

設計変数のスクリーニング

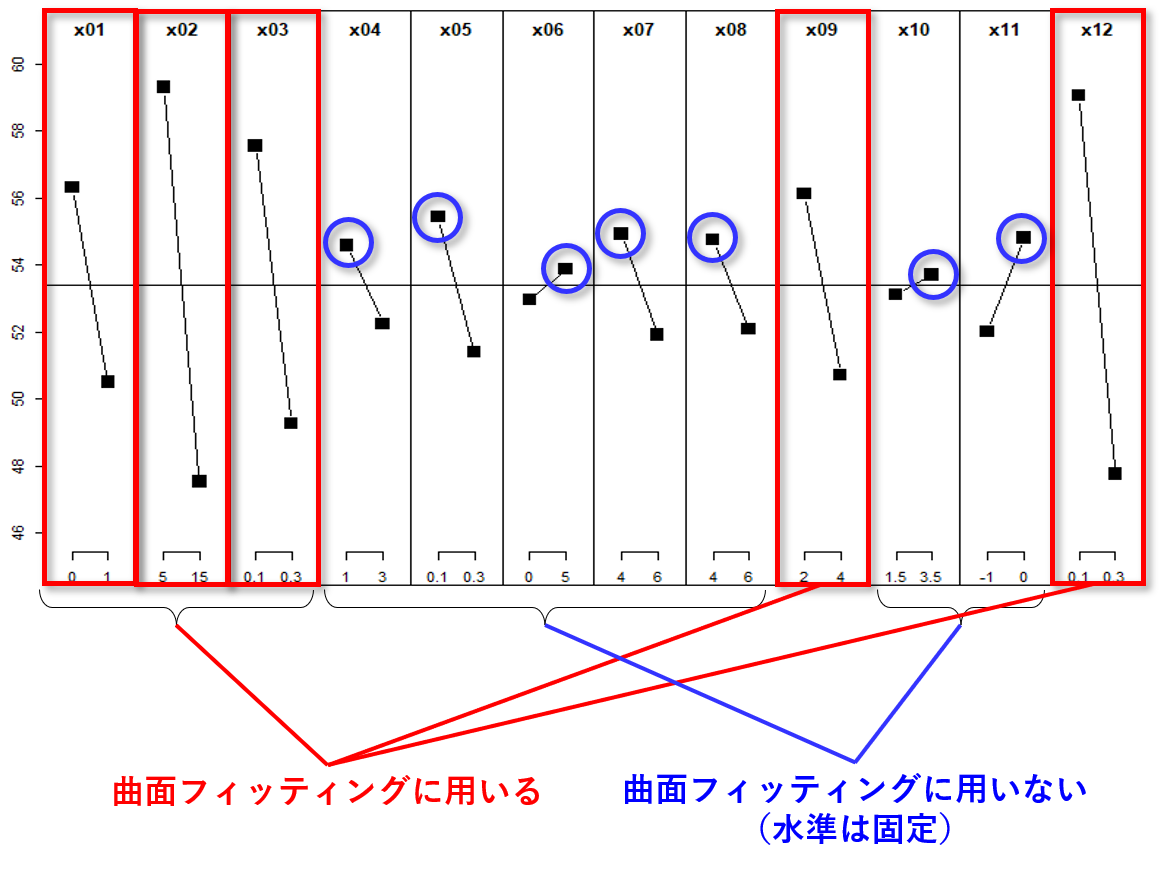
要因効果図中の各線の縦方向の幅は、その設計変数の影響度の大きさを表すことは以前述べたとおりです。それに従うと、影響の大きそうな設計変数は、\(x_1, x_2, x_3, x_9, x_{12}\)になりそうです。
\(x_8\)も\(x_9\)に近いのですが、そう考えてしまってはキリがありません。スクリーニングの選択に明確な正解はありません。今回は、\(x_1, x_2, x_3, x_9, x_{12}\)を残す（曲面フィッティングに用いる）ことにします。目安としていた4つより1つ多いですが、これくらいなら良しとしましょう。

一方、曲面フィッティングに用いない残りの設計変数は、最高高度が高くなる水準で固定します。

なお、スクリーニングする設計変数の選択には、上記の要因効果図を視覚的に見て判断するほか、「分散分析」という手法で判断することもあります。これについては、本記事では説明を省略します。

ちなみに

スクリーニング実験の要因効果図から、「各設計変数において最高高度が高くなる水準」を選択したサンプルにて飛翔シミュレーションを行ってみました。

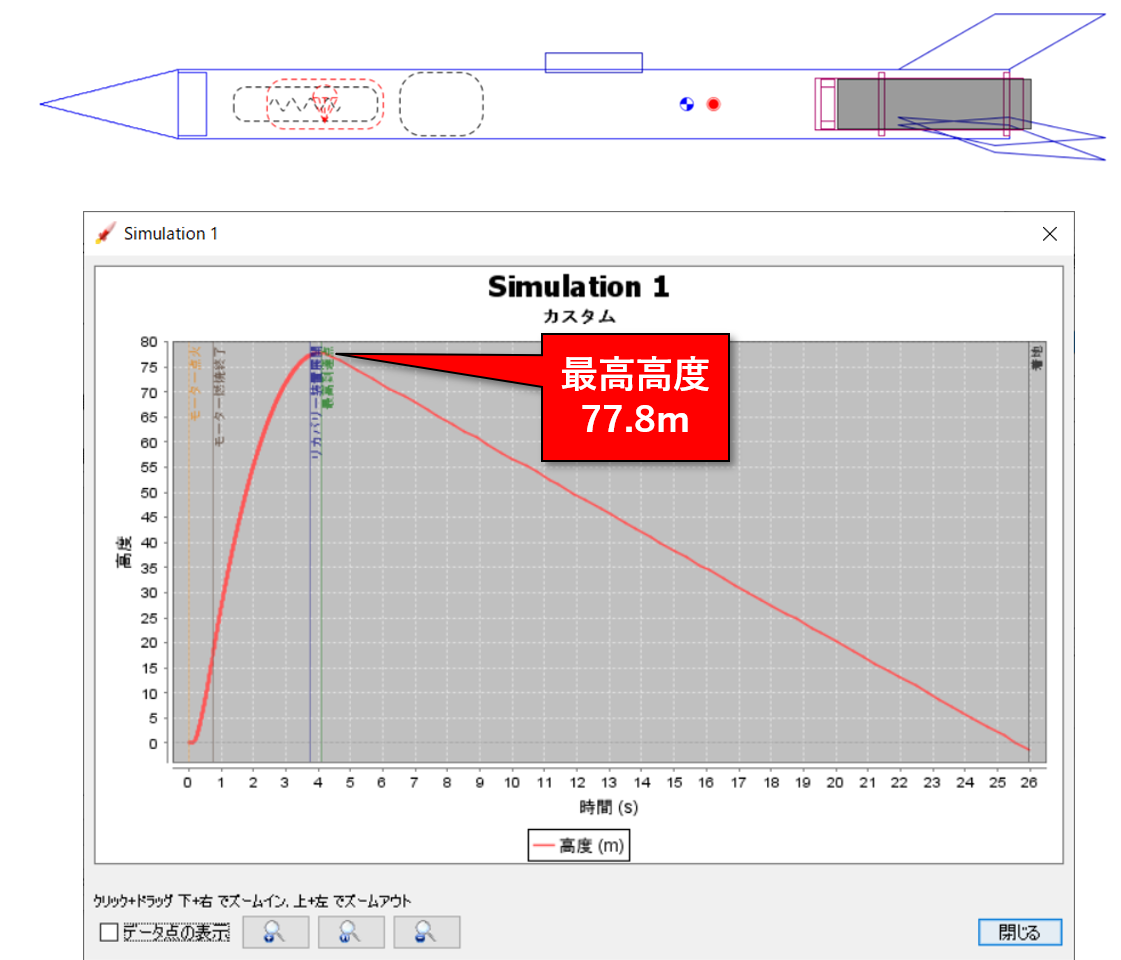
最高高度は、77.8mを示しています。調整前（サンプルファイル）の最高高度が50.5mだったので、これだけでもかなり性能が改善されています。この結果は、次回以降の応答曲面法による最適化における「ベンチマーク」となります。

まとめ

応答曲面法を本格的に適用する前に、影響の大きい設計変数を絞り込むためのスクリーニングについて説明をしました。
なお、これは応答曲面法のみならず、様々なシーンで使うことのできる手法です。

次回は、曲面フィッティングのための実験について説明をします。