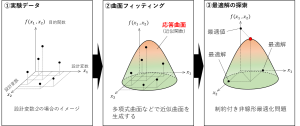
多目的最適化問題(第一回)
パレート解とパレートフロント
多目的最適化問題とは
多目的最適化問題は、複数の目的関数について最適化を行う問題です。
$$f_1(x_1,\cdots,x_n),\cdots,f_n(x_1,\cdots,x_n)$$
上記のように\(n\)個の目的関数\(f_1{\cdots}f_n\)があり、これらをすべて最小化したい場合に用いられます。
なお、以降ではすべての目的関数を最小化する場合について記します。問題によっては最大化したい場合もありますが、その場合は\(-1\)を掛ければ、最小化問題に変換できます。
パレート解とパレートフロント
多目的最適化問題を考える上で、重要な概念が「パレート解」と「パレートフロント」です。
パレート解とは、「理想的な解にできるだけ近く、目的関数同士のバランスが異なる解」のことです。
どういうことでしょうか。2設計変数・2目的関数で説明します。
すなわち、
$$f_1(x_1,x_2),f_2(x_1,x_2)$$
です。
設計変数空間・目的関数空間
設計変数\(x_1,x_2\)は、それぞれ上下限値を持ちます。今、この2つの設計変数が基準化されているとすると、範囲は-1~1です。\(x_1\)を横軸、\(x_2\)を縦軸に取ると、設計変数の取る範囲は以下のように図示できます。
一方、目的関数も同じように2次元平面上に図示できます。すなわち、横軸に\(f_1\)、縦軸に\(f_2\)を取ります。平面上の目的関数の形状は簡単には分かりません。とりあえず、以下のようになると考えておきます。
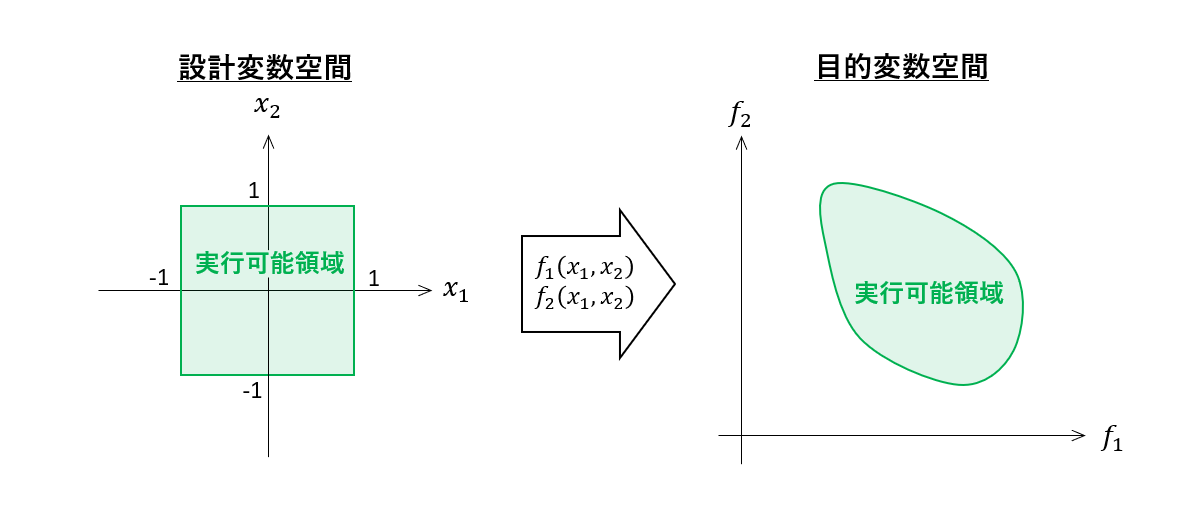
座標軸に設計変数を取った平面(空間)を「設計変数空間」と呼び、目的関数を取ったものを「目的関数空間」と呼びます。
そして、図中の緑色の領域を「実行可能領域」と呼びます。実行可能領域とは、解が取り得る範囲のことです。
パレート解
今、考える問題は、2つの目的関数\(f_1,f_2\)を最小化することです。つまり、目的関数空間で、各軸の負方向に解を探すことになります。
以下の図には、\(f_1\)が最小の点および\(f_2\)が最小の点、および、それらの点の間で実行可能領域の境界上にある点を記しています。
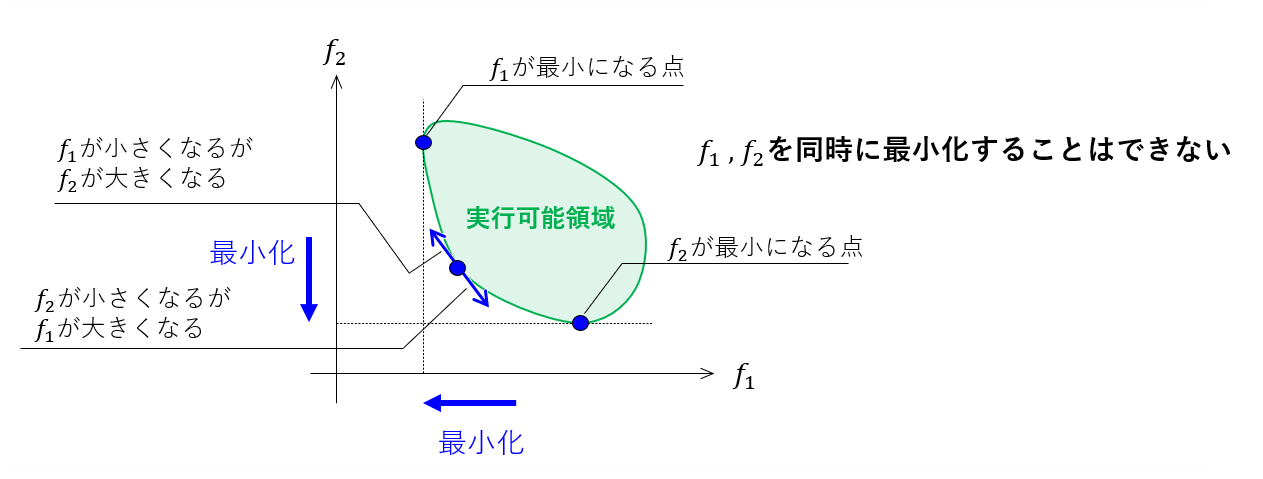
この図から明らかなように、\(f_1,f_2\)を同時に最小化する点は存在しません。
このように多目的最適化問題においては、特殊な場合を除いて、複数の目的関数は"トレードオフ(妥協)"の関係にあります。つまり、解は一意に定めることはできません。
このような解を「パレート解」と言います。
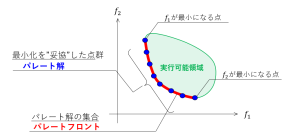
パレートフロント
パレート解は1つではなく、無数に存在します。パレート解の集合は曲線(目的関数が3つ以上のときは曲面)を「パレートフロント」と呼びます。
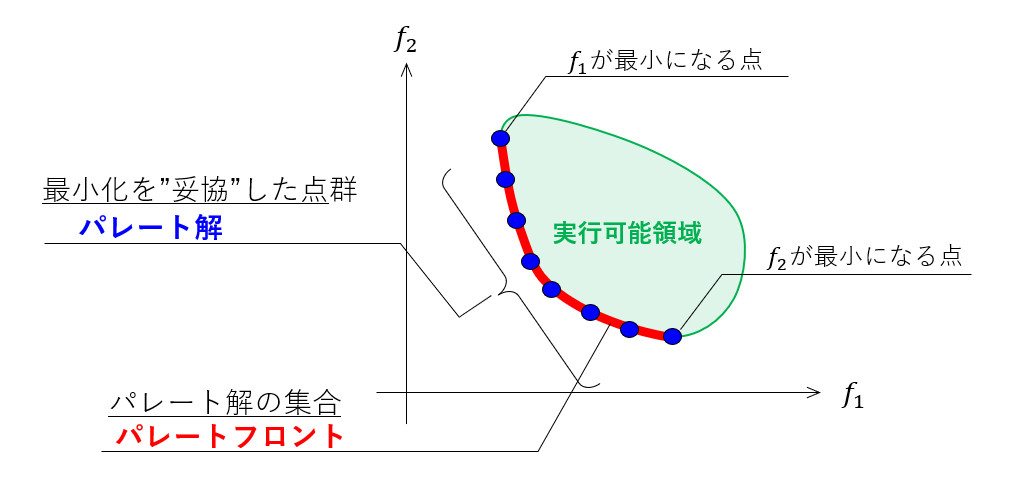
パレートフロントの形状が分かれば、目的関数同士がどのような関係にあるのか知ることができます。関係を把握することによって、設計における何らかの「意思決定」に利用できます。
このように、「多目的最適化問題を解くということは、パレートフロントを求めること」ということになります。
設計対象
ロバストパラメータ設計で用いた構造梁を対象にして、多目的最適化問題のデモを行います。設計対象の詳細は別記事で述べているので、ここでは図で示すのみにします。
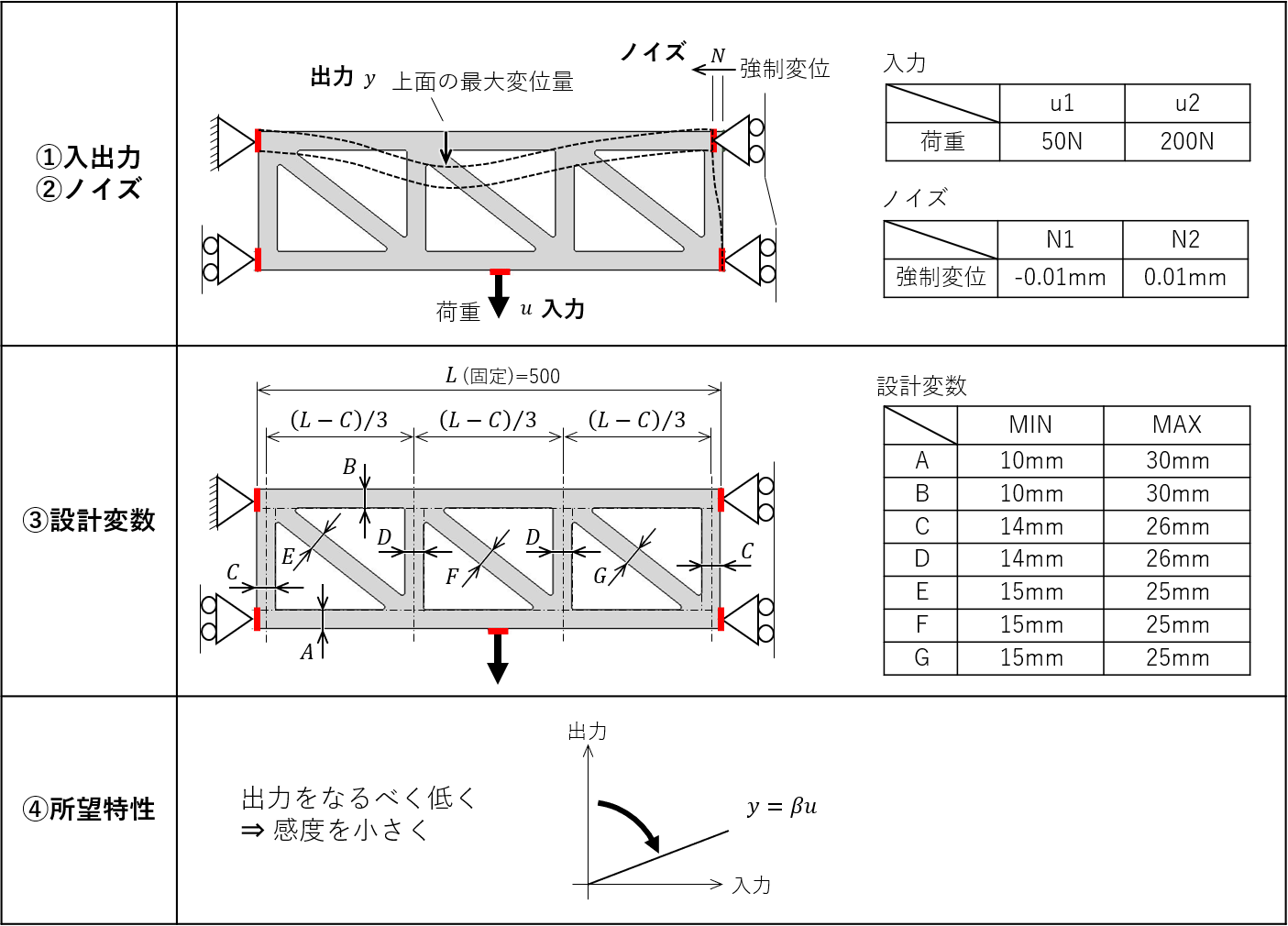
本設計対象はタグチメソッドのロバストパラメータ設計を適用し、実験(シミュレーション)を実施し、感度とSN比の要因効果図を描きました。その結果が以下です。
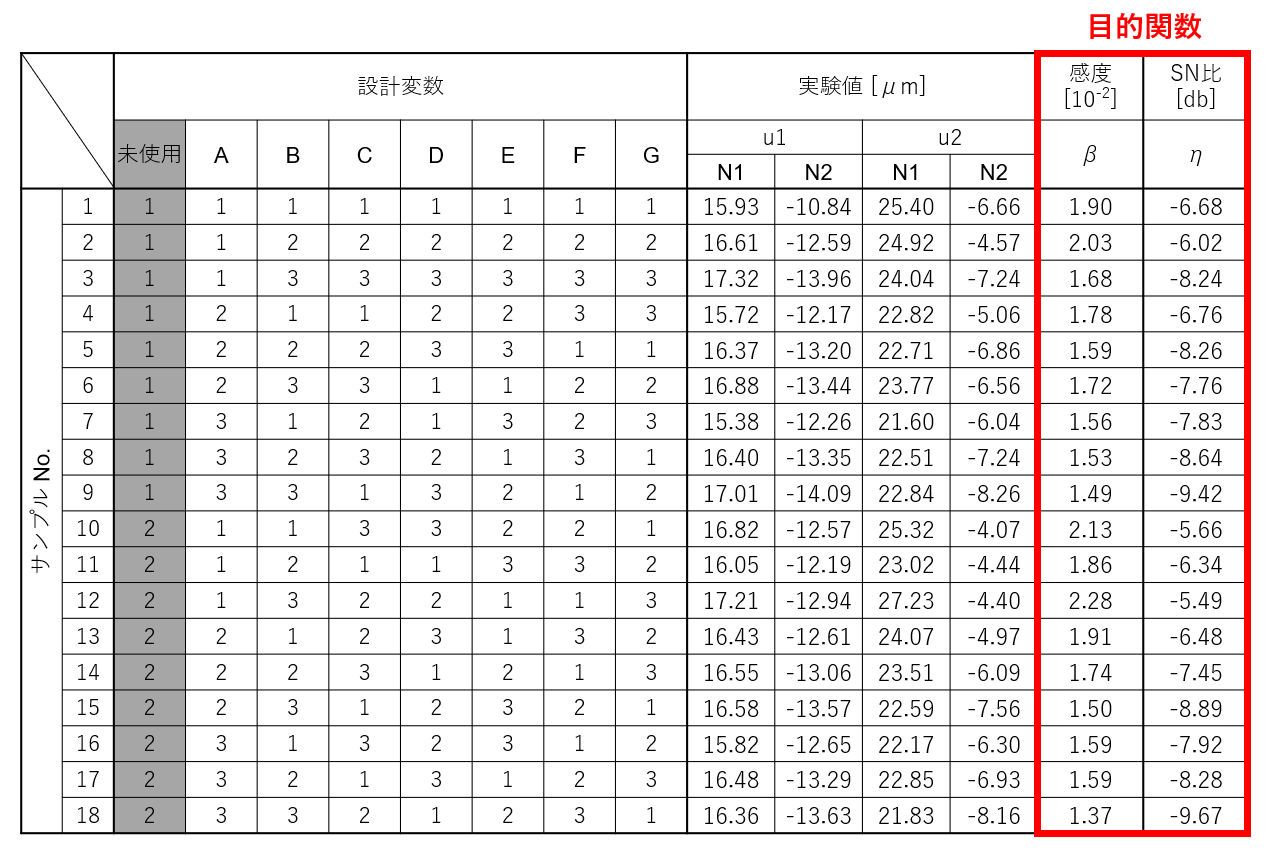
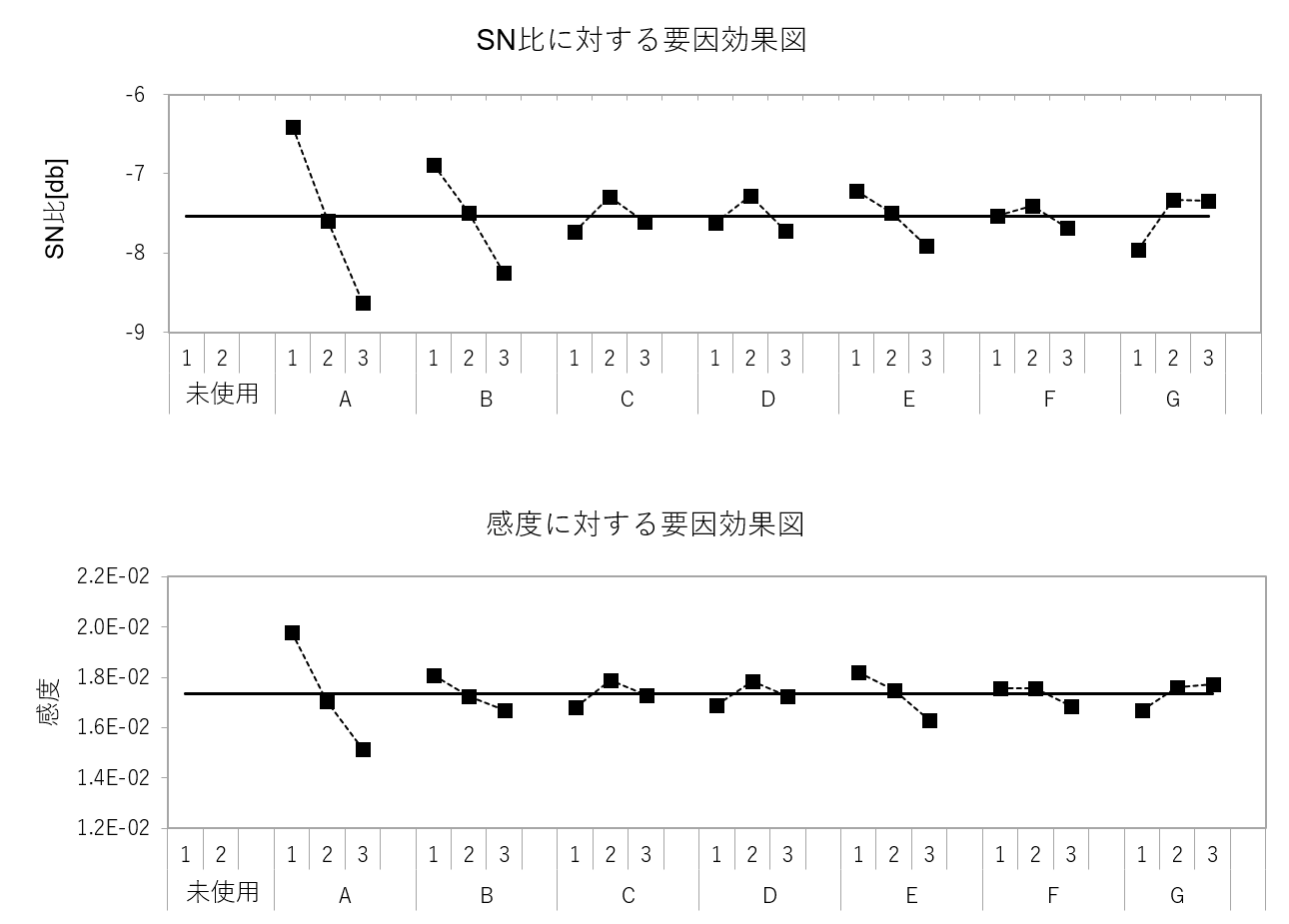
要因効果図より、感度とSN比は同時に最適化できるものではありませんでした。つまり、この場合、感度とSN比はトレードオフの関係にありそうです。
この問題を多目的最適化問題とみなします。すなわち、目的関数は感度とSN比の2つです。感度とSN比を2次元平面上でのパレートフロントを描くことが、この問題のゴールです。そのためのフローチャートは次の通りです。
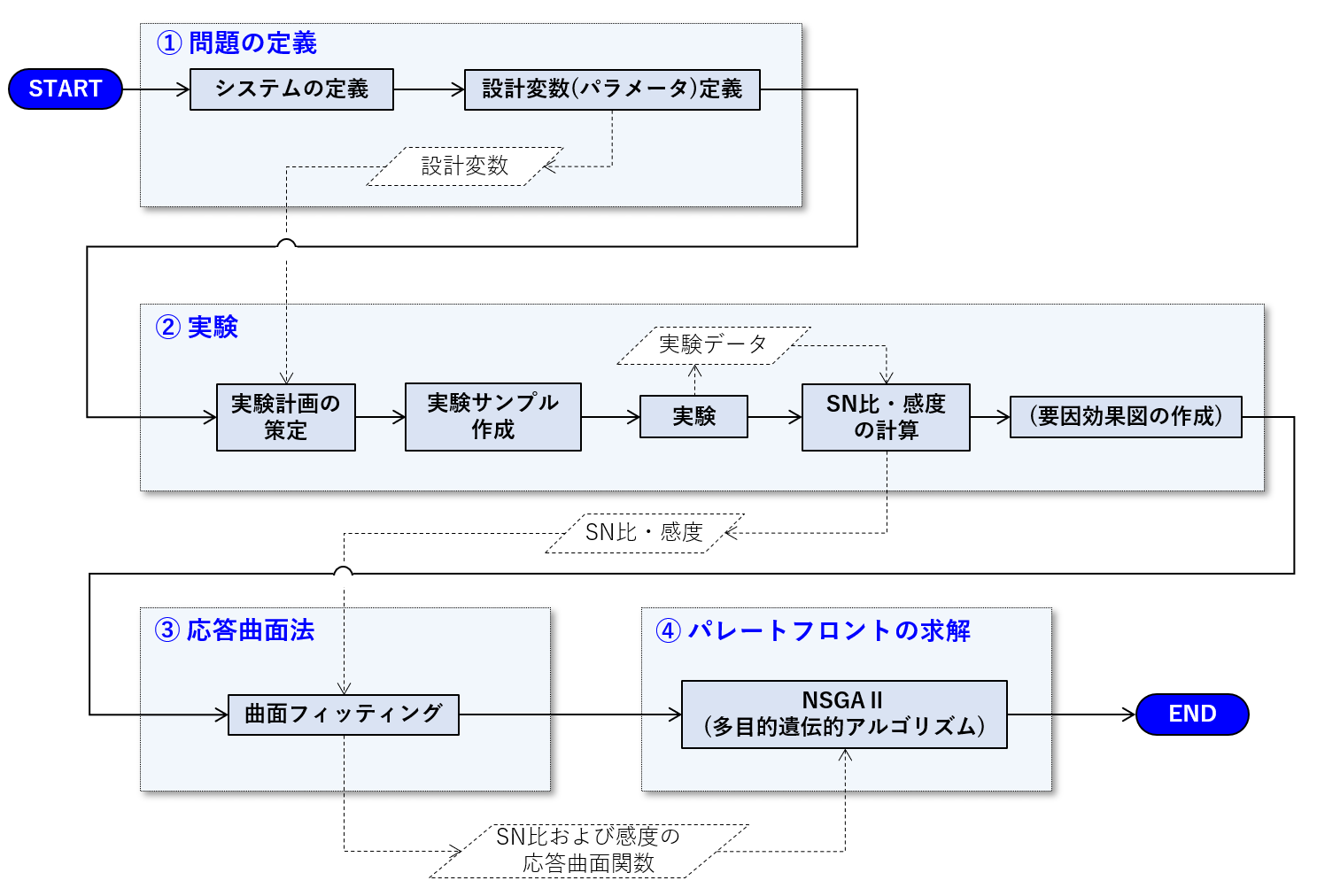
①問題の定義と②実験は、ロバストパラメータ設計のものと同一です。また、実験データも同じものを用います。したがって、すでに完了しています。
残る③および④の詳細は、次回以降の記事にて説明をします。
③応答曲面法
2次関数を適用した応答曲面法については別記事に詳細があります。しかし、今回は2次関数の際に用いた実験計画とは異なる点に注意が必要です。
④パレートフロントの求解
パレートフロントを描くには、いくつかの手法がありますが、ここでは遺伝的アルゴリズムを基礎にした「NSGAⅡ」を紹介します。ただし、本気で説明しようとすると学術論文のような内容になるので、要点のみをかいつまんで行こうと思っています。
まとめ
多目的最適化問題の概要と、パレート解・パレートフロントの概念について説明をしました。
多目的最適化問題のデモ問題はロバストパラメータ設計の際と同じ対象とし、ロバストパラメータ設計で導出した感度とSN比を目的関数にした問題と捉え、これらのパレートフロントを描くことを目標にします。
次回以降では、具体的な手順について説明をしていきます。