多目的最適化問題(第五回)
NSGA-Ⅱによるパレートフロントの求解
前回は、多目的遺伝的アルゴリズム(NSGA-Ⅱ)の説明の前段階として、通常の遺伝的アルゴリズムについて説明をしました。NSGA-Ⅱはこれを応用したもので、多目的最適化問題の求解(パレートフロントの求解)に用いられます。今回は、NSGA-Ⅱについて説明をし、多目的最適化問題のまとめとなっています。
NSGA-Ⅱとは
NSGA-Ⅱとは、「Non-dominated Sorting Genetic Algorithms Ⅱ」の略です。末尾のⅡは、「NSGA」の改良版であることを示しています。「Genetic Algorithm」は遺伝的アルゴリズムのことです。接頭の「Non-dominated Sorting」は「非優越ソート」と訳され、NSGA-Ⅱの大きな特徴です。
NSGA-Ⅱアルゴリズム
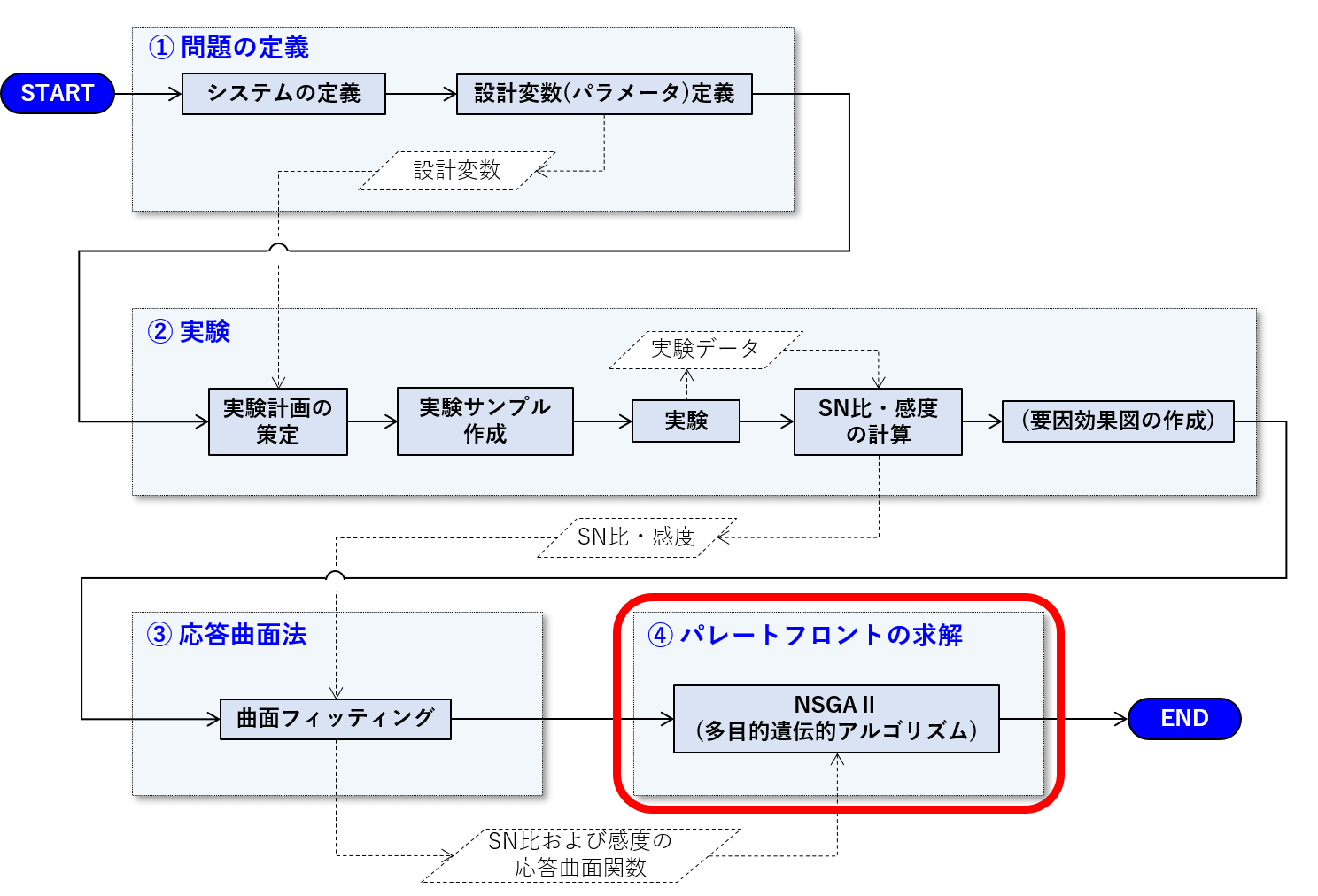
NSGA-Ⅱのフローを以下に示します。

この通り、基本的には通常の遺伝的アルゴリズムと同じです。異なっているのは、個体評価と選択に関する箇所のみです。
個体評価に「非優越ソート」と「混雑度ソート」と呼ばれる方法を用いています。
非優越ソート
非優越ソートについて説明するために、「支配」という概念を説明します。
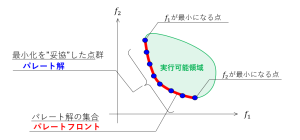
目的関数空間において、ある個体Aから最適化したい方向に、別の個体Bがあったとき、個体Aは個体Bに「支配されている」関係にあります。個体Bは1つとは限りません。このとき、個体Bの方が、パレートフロントに近いと言えます。
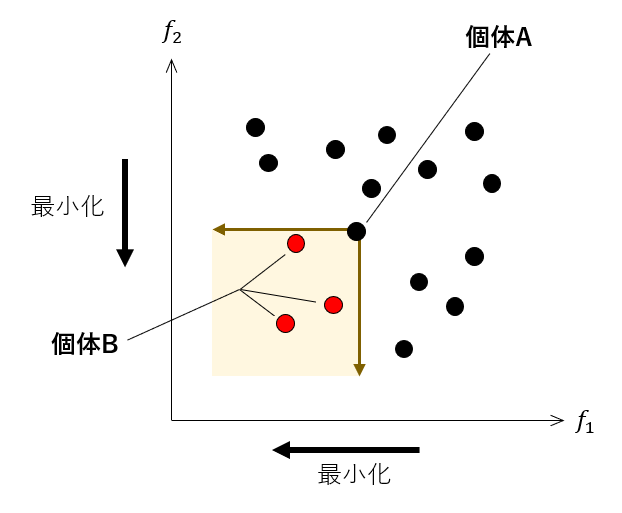
非優越ソートは「支配」の概念を使って、次のように進められます。
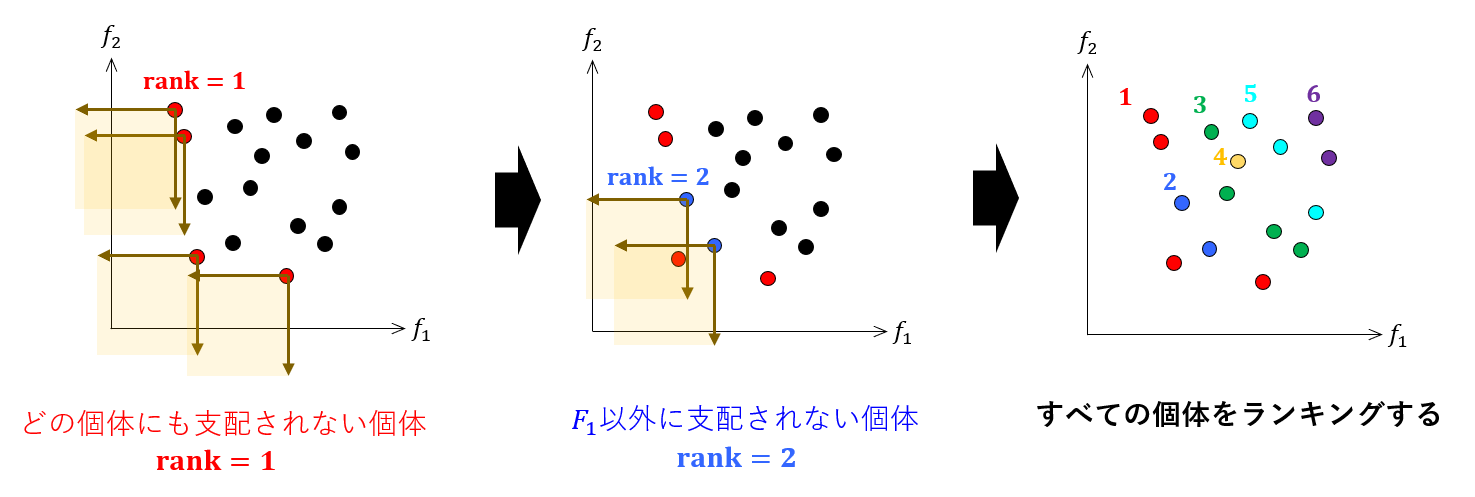
個体群の中から、どの個体にも支配されない個体群を探してランクを付与します。次にランキングされた個体以外において同様に、支配されない個体群を探してランクを付与します。この操作をすべての個体がランキングされるまで、実施します。
言うまでもなく、ランク数が小さい個体がパレートフロントにより近いことになります。つまり、非優越ソートによってパレートフロントへの近さが評価できます。
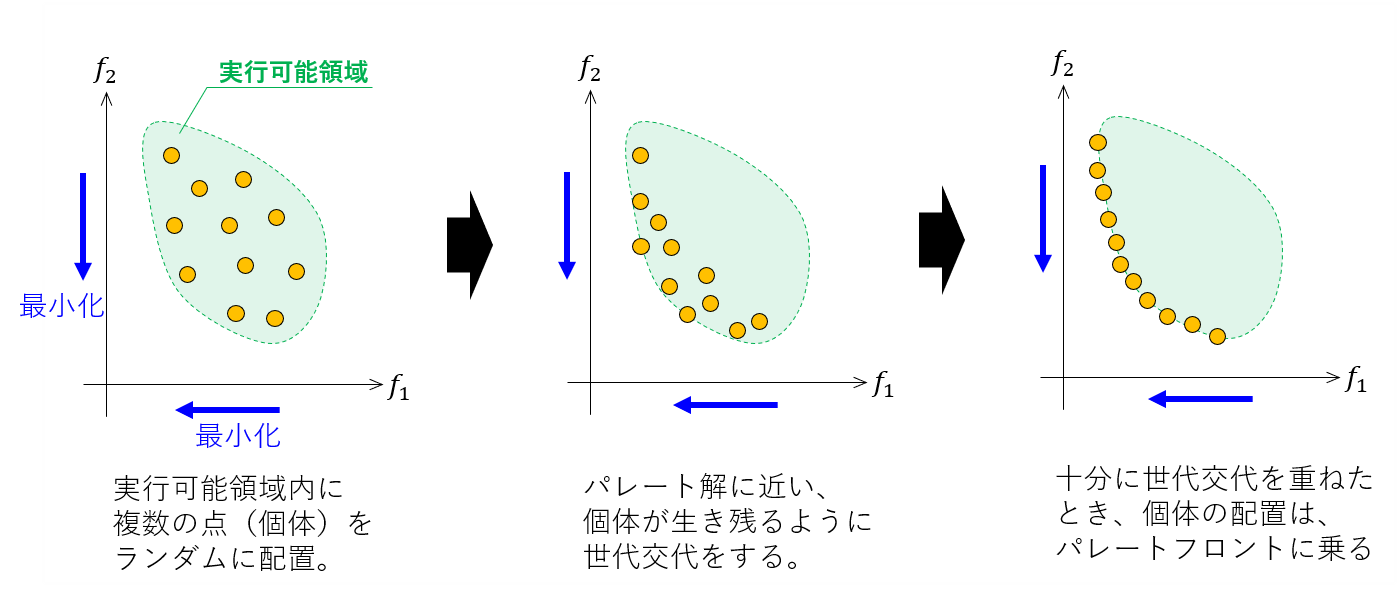
非優越ソートで上位半分の個体を「選択」すれば、世代交代によってパレートフロントが求まりそうです。しかし、同じランクに属する個体の数はコントロールできないので、次のようにちょうど半分の個体を選択することができない場合があります。
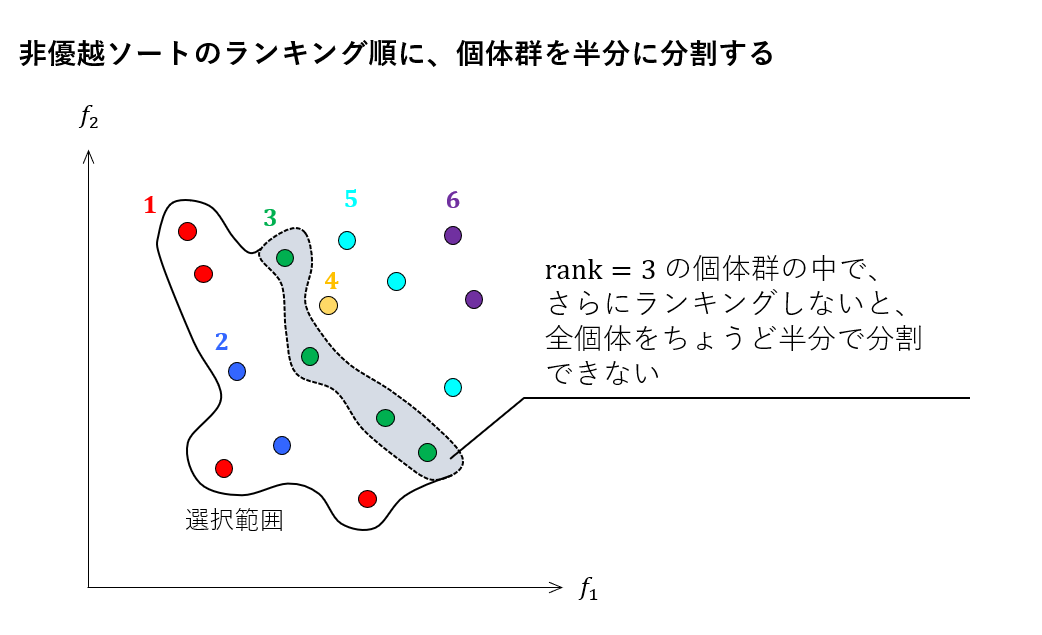
このようなときは、選択の境界に位置するランクの個体群を、さらにランキングしてやる必要があります。
混雑度ソート
あるランクに属する個体群の中で、個体をランキングするときに求められることは「密集していないこと」です。個体は、実行可能領域内でなるべく散らばって分布している方が、求解には都合がよいのです。
そこで、「混雑度」と呼ばれる指標を用いて、個体群をランキングします。これを「混雑度ソート」と呼びます。
混雑度は、次の例のように計算されます。
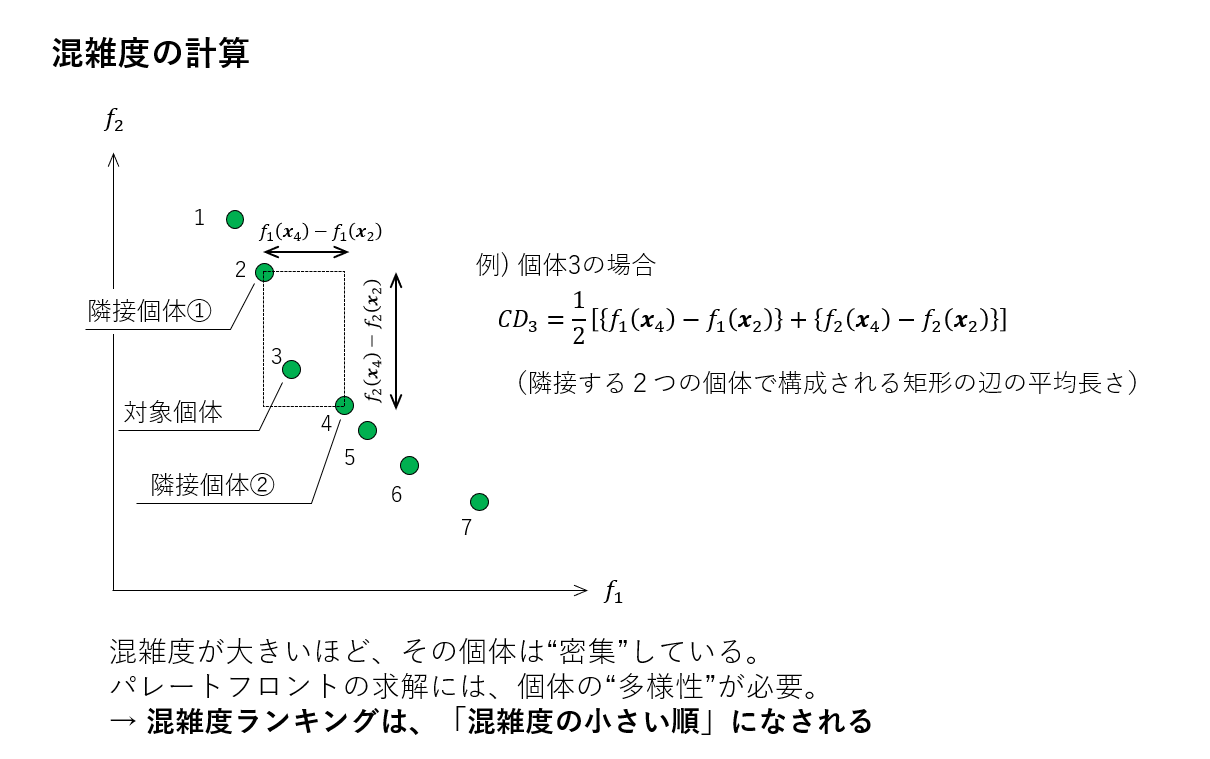
上の例は2目的関数の例です。\(i\)番目の個体についての混雑度計算の一般式は以下のようになります。
$$CD_i = \frac{1}{k}\sum_{j=1}^{k}{\left| f_j(\boldsymbol{x}_{i+1})-f_j(\boldsymbol{x}_{i-1})\right|}$$
\(k\)は目的関数の数です。
進化計算ループ
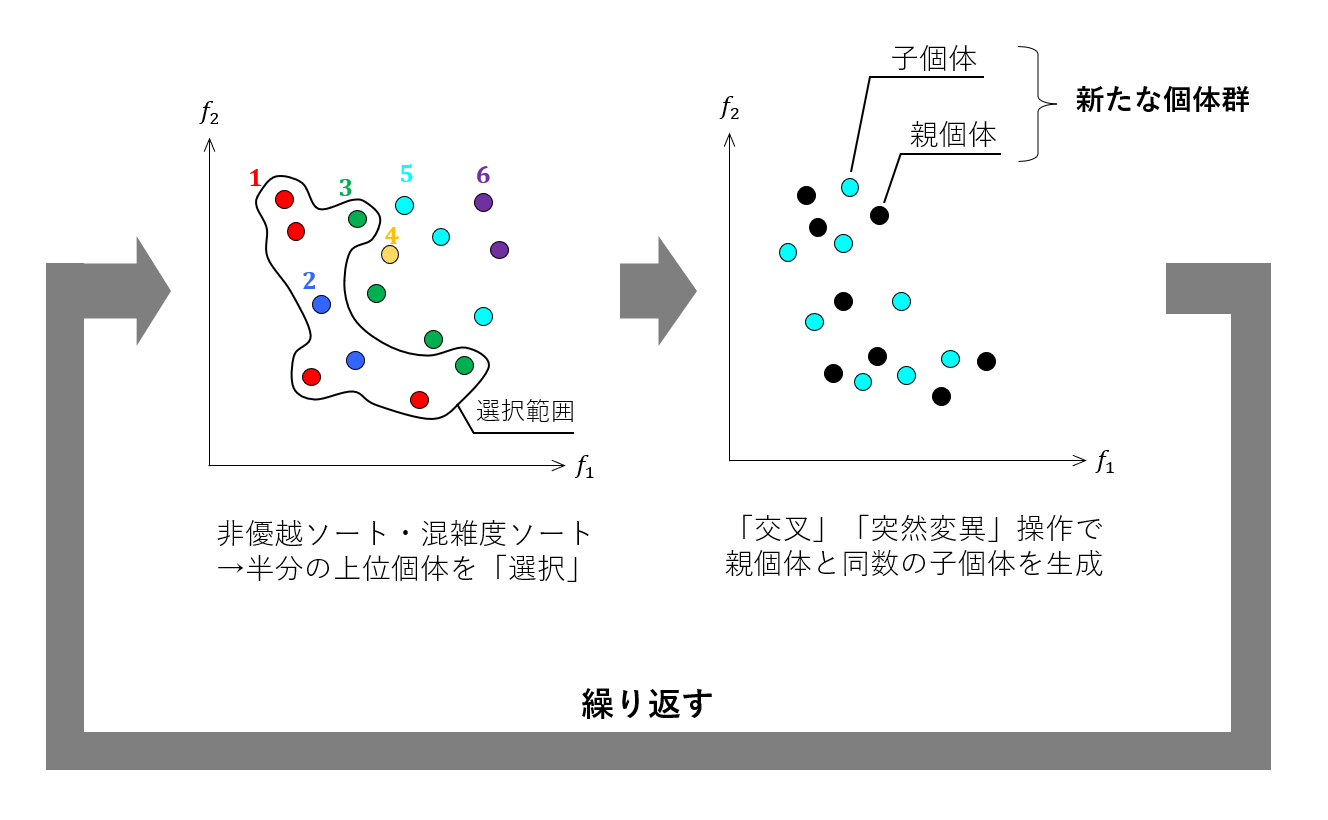
非優越ソートと混雑度ソートによって、個体群は半分ごとに二分されます。ここで、上位半分を「選択」します。このように評価の順によって選択することを「エリート選択」と呼びます。
世代交代の操作の内、「交叉」と「突然変異」は、通常の遺伝的アルゴリズムと変わりません(逆に言うと、方法によってさまざまなバリエーションがあります)。選択後の個体群を親として、交叉・突然変異操作を行い、子個体群を生成します。親個体群と子個体群を合わせた個体群に対して、再度、非優越ソートを行います。NSGA-Ⅱでは、このループを指定回数繰り返します。
パレートフロントの求解
NSGA-Ⅱを用いて、デモ問題のパレートフロントを求めてみます。デモ問題については、第一回の記事で述べています。
目的関数は「感度」「SN比」の2つです。これらは応答曲面法によって、以下のRBFネットワークの数式で表されています(第三回記事)。
$$y=f(\boldsymbol{x})=\sum_{j=1}^{m}{{\alpha}_j \cdot K(\boldsymbol{x}, \boldsymbol{w}_j)}$$
$$K(\boldsymbol{x}, \boldsymbol{w}_j) = {\rm{exp}}\left\{ \frac{(\boldsymbol{x}-\boldsymbol{w}_j)^T(\boldsymbol{x}-\boldsymbol{w}_j)}{{r_j}^2}\right\}$$
NSGA-Ⅱを実行するプログラムについては詳細を省略しますが、Pythonのライブラリ「pymoo」を使用しています。
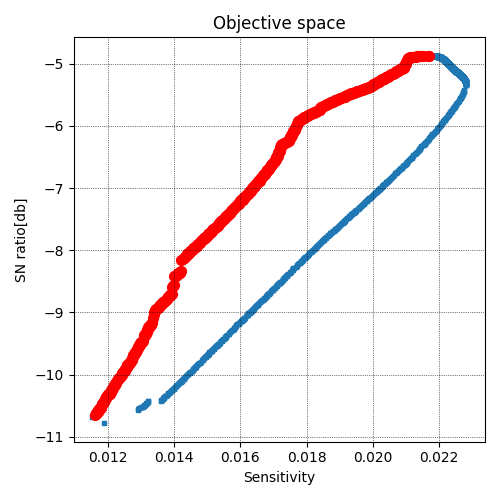
以下が、パレートフロントの求解結果です。横軸に感度、縦軸にSN比を取った目的関数空間です。
赤い点(曲線のように見えますが、個体の点プロットです)がパレートフロントです。青い点は実行可能領域で、各目的関数の正負を入れ替えた、それぞれのパターンにてNSGA-Ⅱを実行することによって得ることができます。ところどころで途切れている箇所がありますが、実行可能領域およびパレートフロントの形状が掴めると思います。
設計対象の要求特性は、「感度を低く」と「SN比を大きく」でした。パレートフロントの形状を見ると、この2つの特性の両立は著しく困難であると分かります。ロバストパラメータ設計では、要因効果図からこのような結果を推測していましたが、パレートフロントを描くことによって、より明確になったと言えます。
ロバストパラメータ設計の記事でも考察していますが、やはり、要求されている事柄に対して、構造が良くない(設計が悪い)と言わざるを得ません。
まとめ
全5回にわたり、多目的最適化問題について説明をしました。
解法にあたり、理論が難解なところはありますが、1つ1つの計算は至極単純です。また、最近ではPythonなどのライブラリも無償で使うことができます。実際に、パレートフロントの求解まではプログラムを作成すれば、ほぼ自動で実施できます。
多目的最適化問題で求解される結果は、パレートフロントの形状のみです。デモ問題の結果からも分かるように、これだけで設計が決まるわけではありません。重要なことは、パレートフロントの形状から、情報を読み取って考察することで、次の一手を見出すことです。
多目的最適化問題など、設計ソリューションの実務作業等を請け負っています。
詳細は、問い合わせフォーマットにて受け付けています。