ロバストパラメータ設計(第三回)
実験計画と実験
第三回目からは、実験について説明します。今回は、実験計画と実験についての説明です。
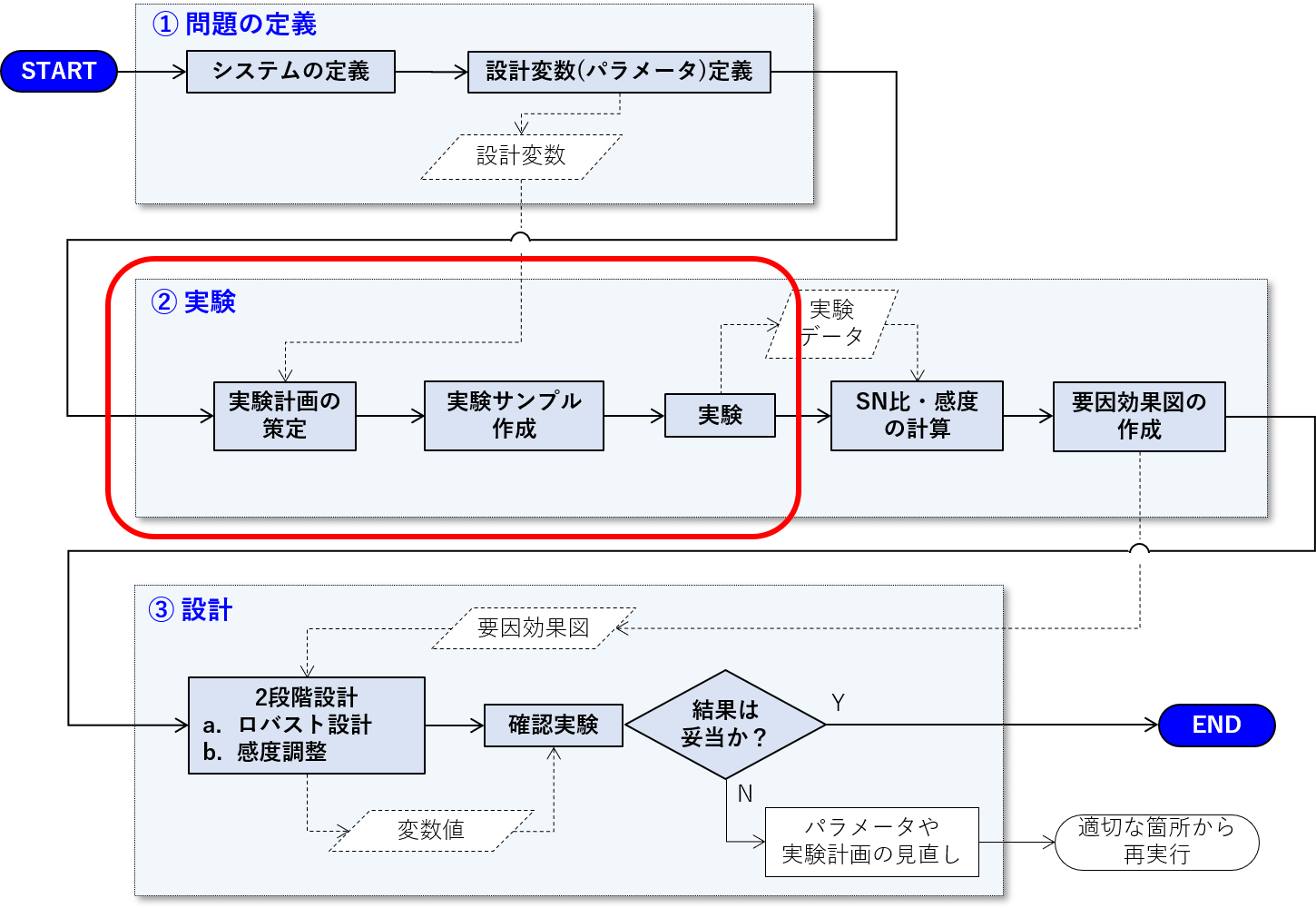
フロー図で示すと、下記の赤枠で囲ったところです。
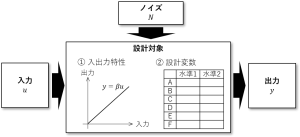
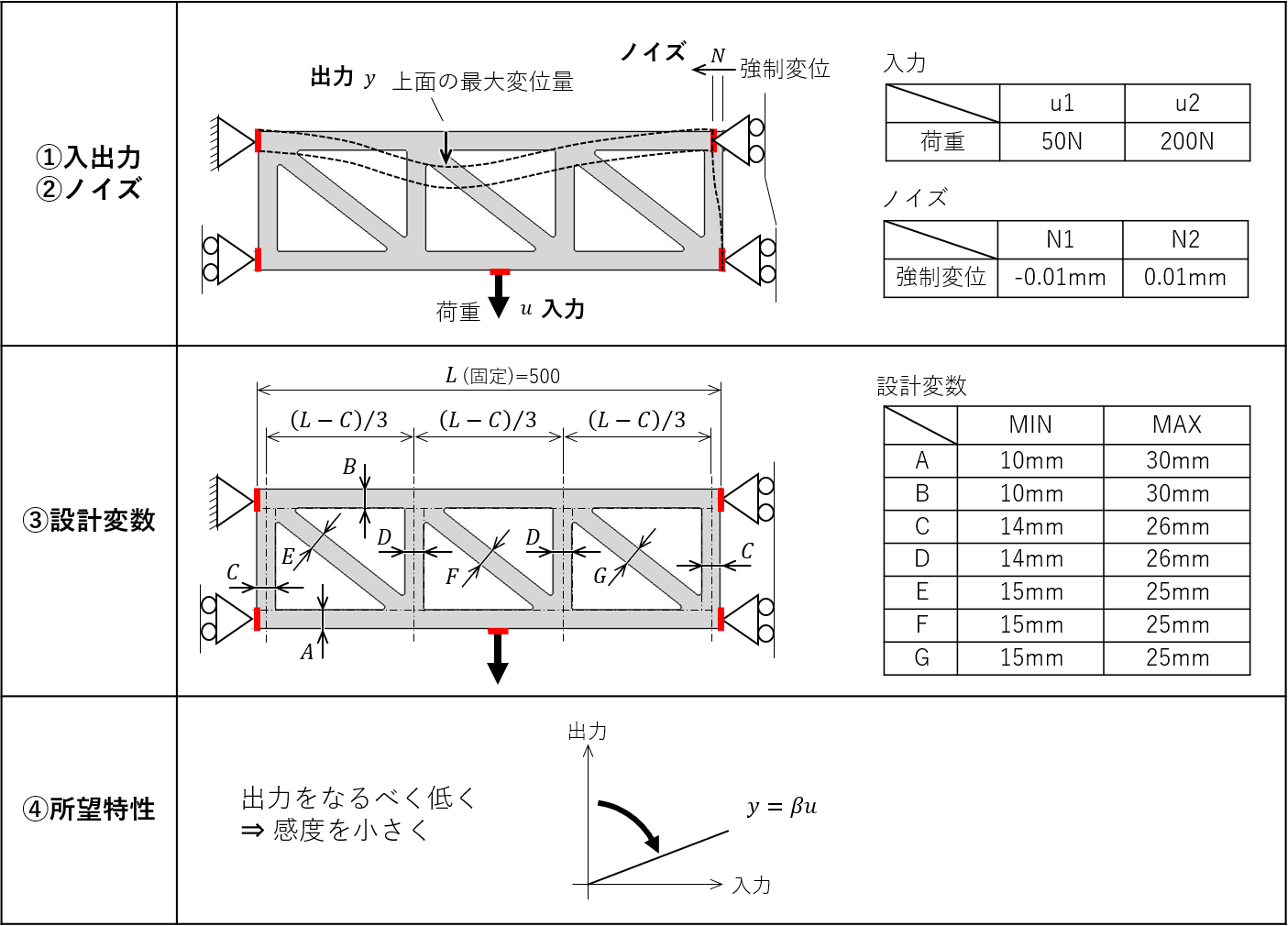
そして引き続き、前回設定した設計対象について考えて行きます。前回は、下図のように問題の定義まで行いました。
実験計画
サンプルの作成
実験数について
ロバストパラメータ設計は実験を通して、設計変数の値を決めて行く技法です。
設計変数を種々に変えたサンプルを作成して出力値を測定するのですが、どのように設計変数を変えて行けば良いのでしょうか。
今回の設計対象には、7個の設計変数があります。それぞれ上下限値を定めていますが、取り得る値は無数に存在します。仮に各設計変数ごとで2つの値を取ったとしても、その組み合わせは、\(2^7=128\)通りもあります。
シミュレーションであれば、プラグラミングで自動計算できるかもしれませんが、それでもかなりの時間と労力が必要です。
直交表
ここで、効率よく実験を進めるために「直交表」を使用します。
直交表には様々なものがありますが、タグチメソッドでは「混合系」と呼ばれるものが使用されます。
直交表についての詳しいことは、いずれ別の記事にしようと思っています。ここでは使い方についてのみ説明をします。
今回用いるのは、下図の「混合系直交表\(L_{18}\)」と呼ばれる直交表です。

この直交表の特徴を簡単に記します。
直行表の「行」
直交表の「行」は、実験のためのサンプルを表します。すなわち、この直交表の行数は18なので、18個のサンプルが作られます。
直行表の「列」
一方、直交表の「列」は、設計変数を表します。混合系直交表\(L_{18}\)は8列から構成されます。今回の設計対象は7個の設計変数を有しているので、このサイズの直交表を使います。
このように、設計変数の数によって使われる直交表を選定することになります。
\(L_{18}\)のほかには、\(L_{12}\)や\(L_{36}\)があります。詳しい説明は省きます。興味がある方は、検索すればすぐにヒットすると思うので各自調べてみてください。
直行表の要素
直交表の「要素」は、設計変数の「水準」を意味します。
混合系直交表\(L_{18}\)は、1列目は\(1{\sim}2\)で、2列目以降は\(1{\sim}3\)から成ります。これが「混合系」と呼ばれる所以です。
タグチメソッドのロバストパラメータ設計では、このような混合系直交表を用いることが推奨されています。
設計変数の割り当て
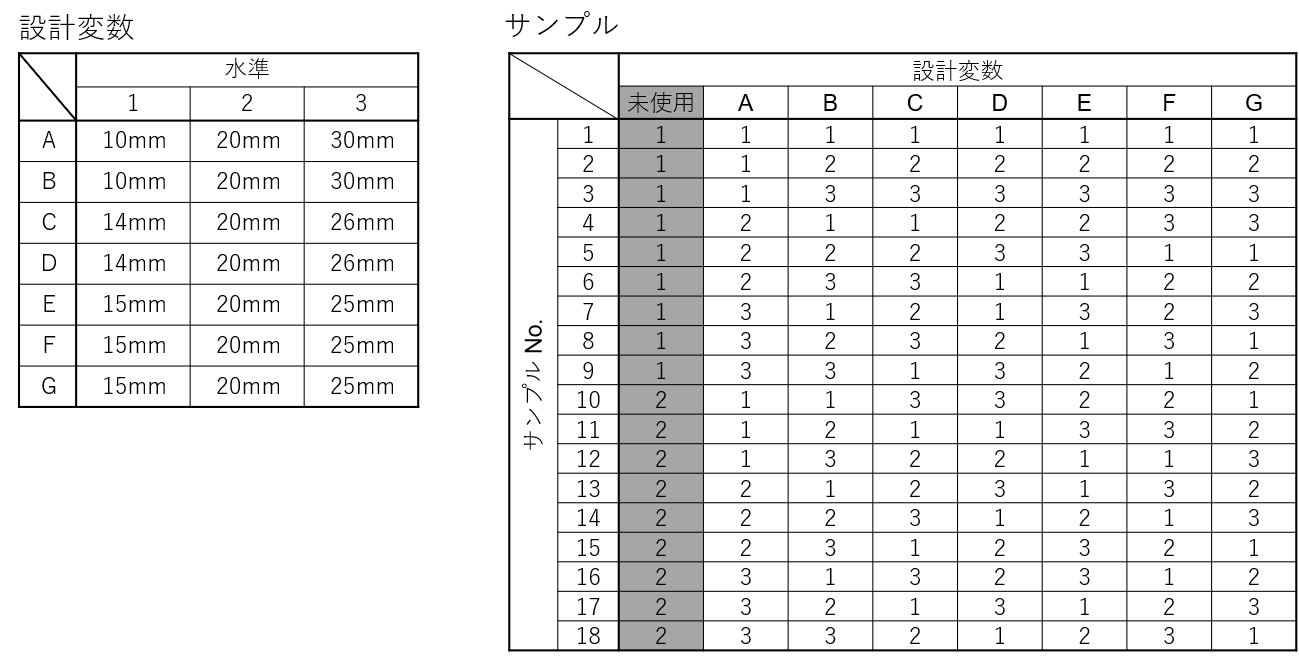
実際に列に各設計変数を割り当ててみます。
各設計変数には、上下限値が定義されています。新たにその中間値を加えて、「水準1:下限値、水準2:中間値、水準3:上限値」とします。
そして、第2列から第8列に設計変数A~Gを割り当てます。第1列には何も割り当てません。直交表を使う際は、未割当列を最低1つは残す必要があります。
実験条件の設定
次に実験条件を設定します。
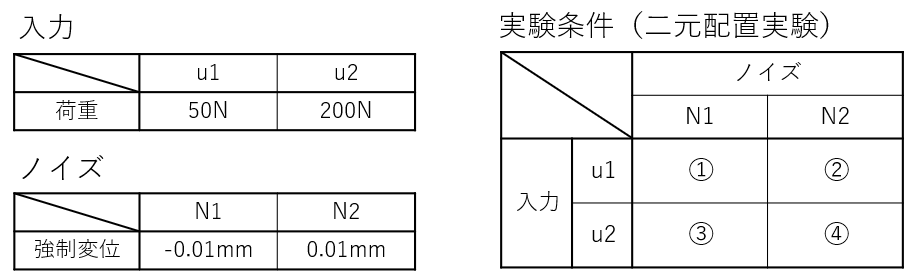
ここでいう条件とは、入力とノイズの条件になります。この2つについても、上下限を定めているので、下図のように条件を設定します。
入力とノイズでそれぞれ2水準を取り、4パターンの組み合せとしています。このように水準を取る実験を「二元配置実験」と言います。
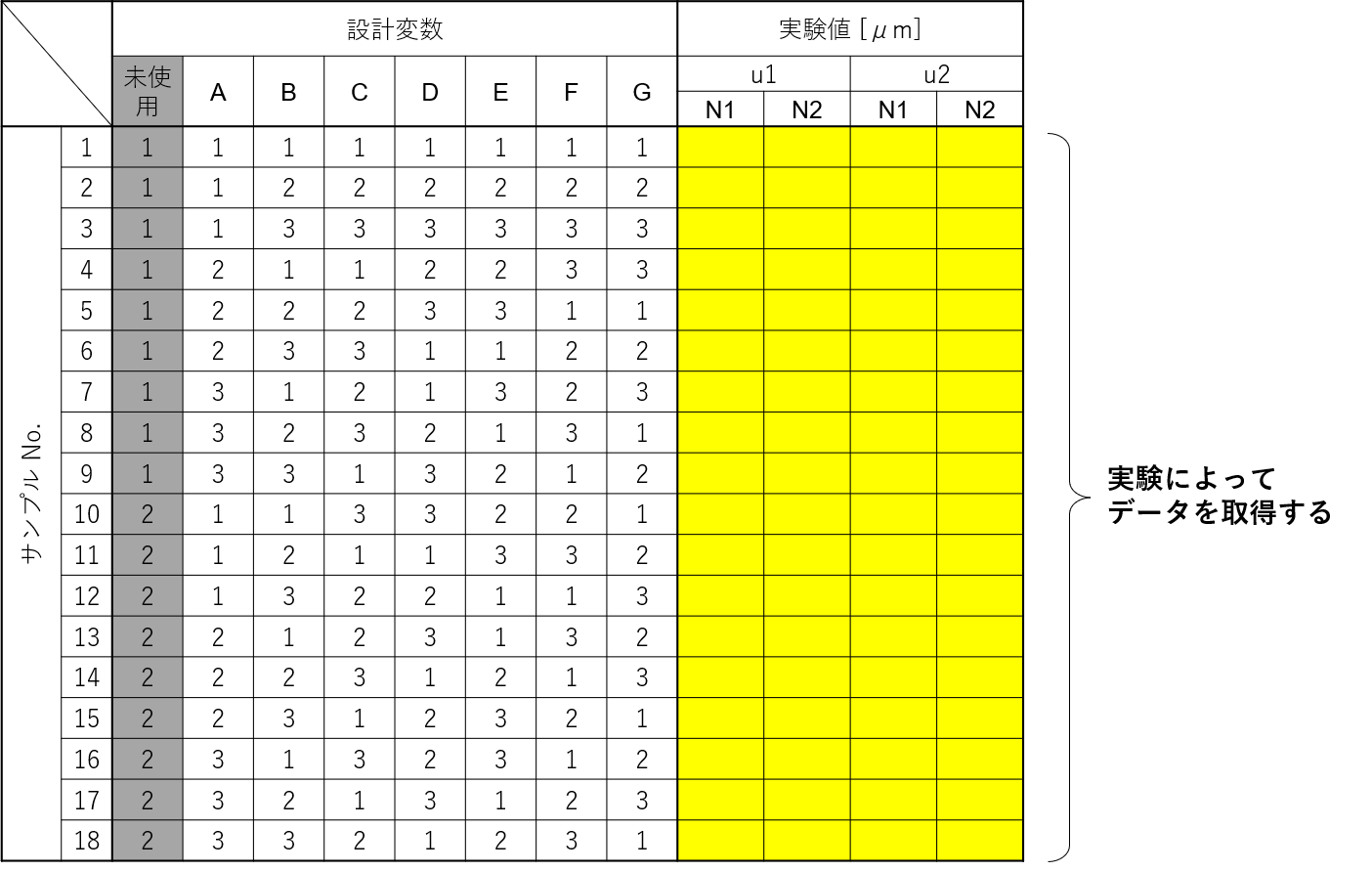
以上、サンプル作成と実験条件の設定により、実験計画が完成します。まとめると以下の表になります。
サンプル1個につき、4条件でのデータ取得を行う計画になっています。
実験
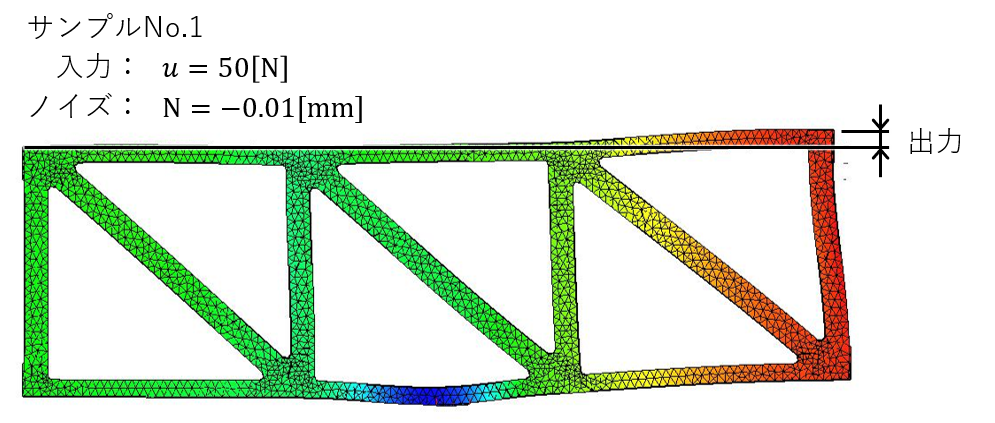
本デモの実験は、構造解析ソフトウェアを用いたシミュレーションとします。シミュレーション結果の一例を以下に示します。上面の最大変位は右端に現れています。なお、材質はスチールです。
なお、モデリングと解析にはフリーの「FreeCAD」を使用しました。
これはフリーの3D-CADで構造解析まで行うことができます。オープンソースで開発途上とのことですが、フリーソフトでここまでできるようになったとは、良い時代になったものです。また、このCADソフトは、Pythonのスクリプトで操作ができるようです。今回のように多数のモデリングや解析を実行する場合、上手くコーディングできれば、大幅に工数の削減ができそうです(まだそこまで使いこなせていませんが)。
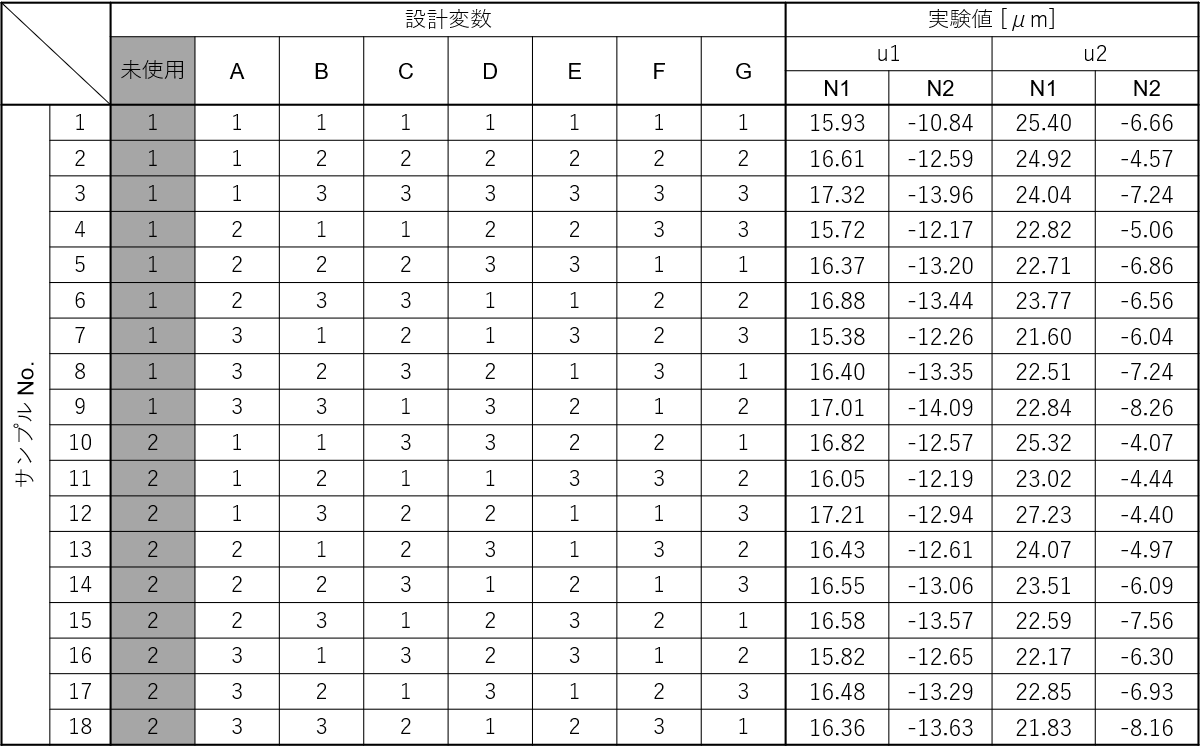
すべてのサンプルの各条件でシミュレーションを行った結果、下表のようになりました。
まとめ
ロバストパラメータ設計における、実験計画と実験について説明をしました。
この作業は、適切に問題の定義ができていれば、比較的システマティックに進むと思います。全条件の実験(シミュレーション)の実施は大変ですが、闇雲に条件を定めるよりは遥かに効率的です。その威力は次回以降の記事で明らかになります。
次回は実験結果の処理について説明をします。