ロバストパラメータ設計（第四回）
実験データの処理

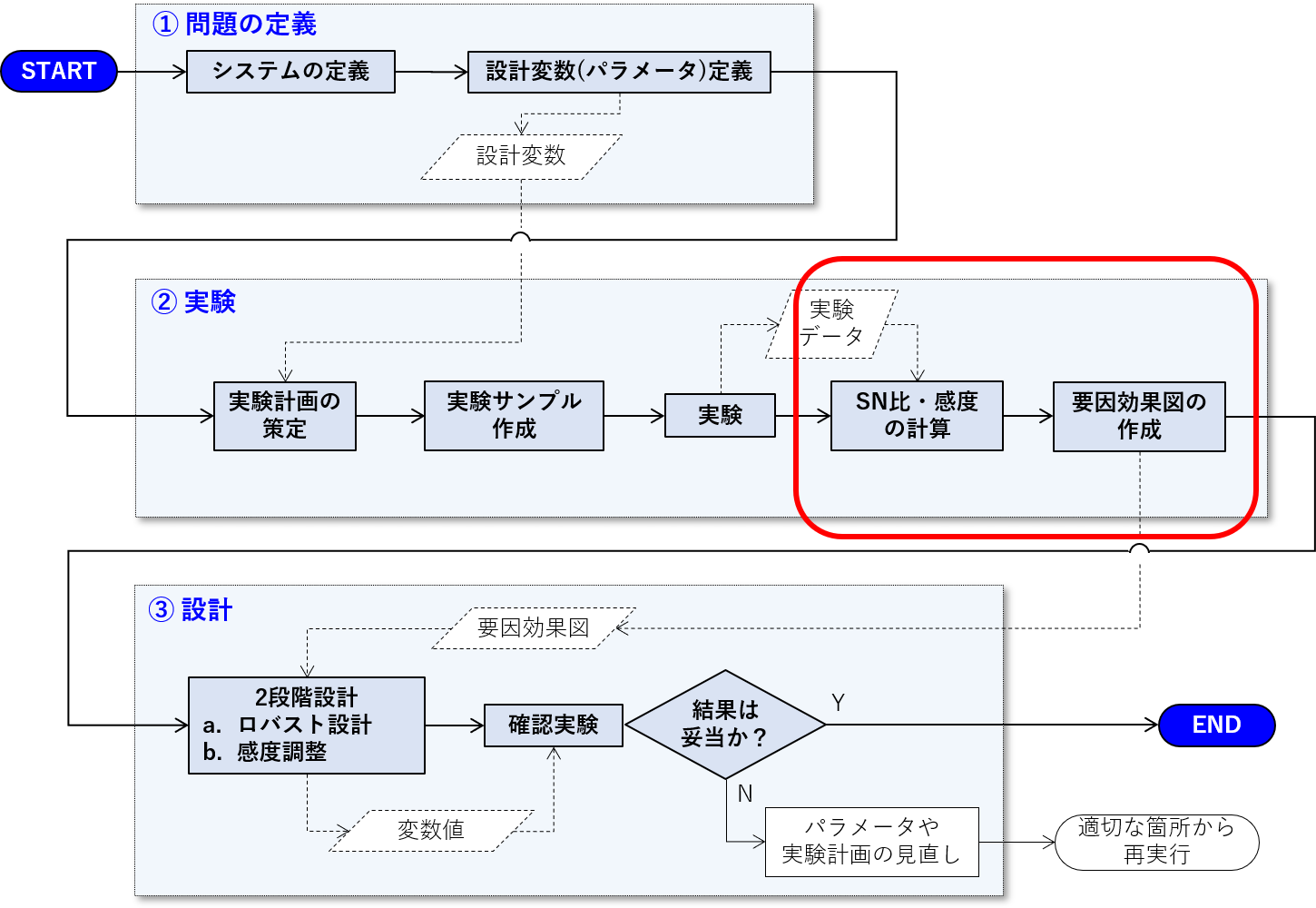
ロバストパラメータ設計の四回目となる本記事では、実験データの処理について記述します。下の作業フロー中の赤枠内になります。

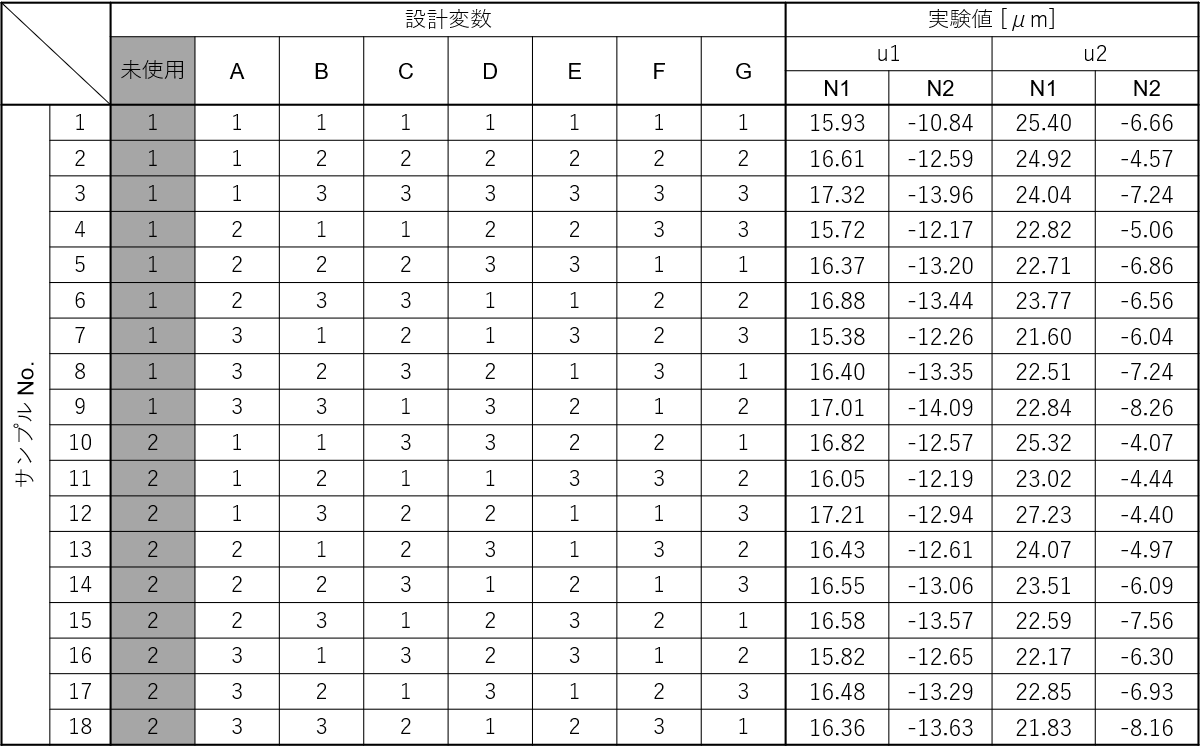
前回は、下表のように実験計画を立てて実験データを取得するところまで説明しました。今回は、パラメータ設計のために、これらのデータを処理する内容になります。具体的には、①感度・SN比の計算、②要因効果図の作成の2つです。

感度とSN比の計算

感度とSN比は、ロバストパラメータ設計で調整の対象になる指標です。
感度とは、入力と出力の傾き(比例係数)のことでした（第一回参照）。一方、SN比とは、ロバスト性の指標になる量です。

感度の計算

感度・SN比の計算をする際は、直交表の「行」に注目します。
1つの行には、4つの実験値(出力)が存在しています\((y_{11}, y_{12}, y_{21}, y_{22})\)。入力とのセットで考えると、\((u_{1}, y_{11})\)、\((u_{1}, y_{12})\)、\((u_{2}, y_{21})\)、(\(u_{2}, y_{22})\)の4つの点があることになります。
これらの4つの点に、最もフィットする直線\(y={\beta}u\)を求めれば、そのときの\(\beta\)が感度になります。最小二乗法を用いれば、この直線は簡単に求まります。

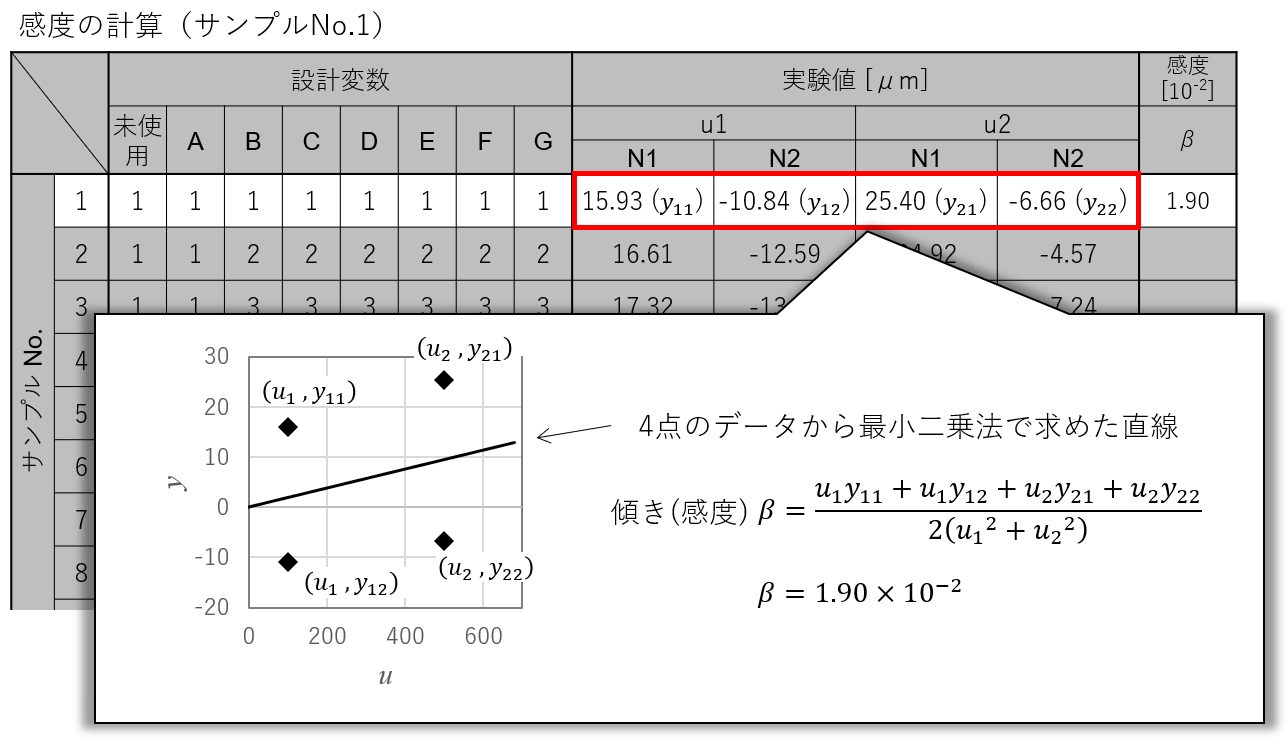
この手順をすべての行に適用し、各サンプルにおける感度を計算します。なお、このような直線は回帰直線と呼ばれます。

SN比の計算

SN比は、一般に信号解析の分野では、信号とノイズの比率を表した数値で、信号の"品質"の指標として良く用いられます。
品質工学では、入力による変動とノイズによる変動の比率から計算されます。ノイズによる変動だけでなく、入力による変動も含んでいるのは、入力とノイズの大きさの相対関係を考慮しているためです。

このことから、SN比を計算するためには、まず「変動の分解」という作業が必要になります。

変動分解

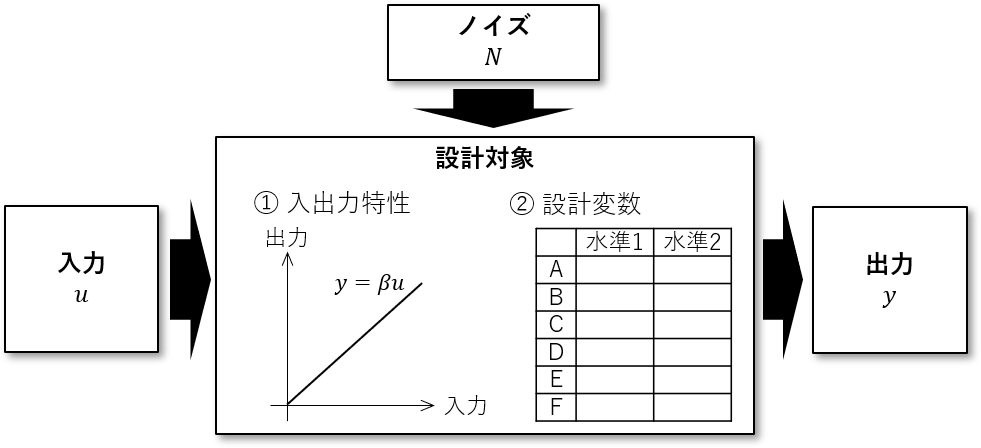
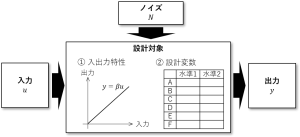
最初に設計対象を下のようなシステム図で表しました。

入力とノイズによって、システムの出力が発生するという構造をしています。
つまり、「システムの出力は、入力とノイズによって"変動"する」と考えることができます。変動分解とは、変動を「入力によるもの」と「ノイズによるもの」とに分解する作業になります。具体的には、「全変動」、「回帰変動」、「残差変動」の3つの量を計算することでを求めます。

全変動

最初に、入力・ノイズの分解を考えない「全変動」を求めます。全変動は、\(y=0\)からの各実験データまでの変動で表されます。

全変動\(S_T\)は、全実験データの2乗和で計算することができます。

$$S_T=\sum_{i=1}^{2}{\sum_{j=1}^{2}{{y_{ij}}^2}}$$

回帰変動

次に回帰変動です。
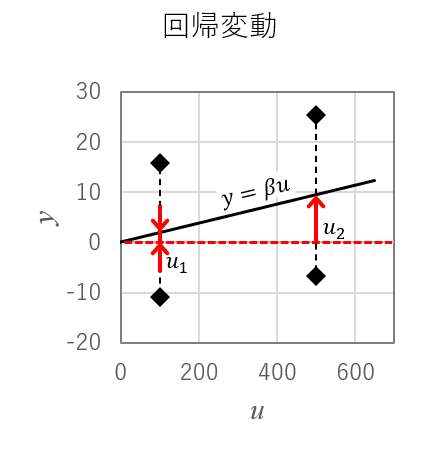
感度の計算の際に、4つのデータから回帰直線を求めました。回帰変動とは、\(y=0\)から回帰直線までの変動になります。

回帰変動\(S_{\beta}\)は、出力=0から回帰直線までの距離の2乗和で計算されます。

$$S_{\beta}=2\sum_{i=1}^{2}{({{\beta}u_{i}})^2}$$

2倍しているのは、全変動とデータ数を合わせるためです。
回帰変動は、「入力による変動」と考えることができます。

残差変動

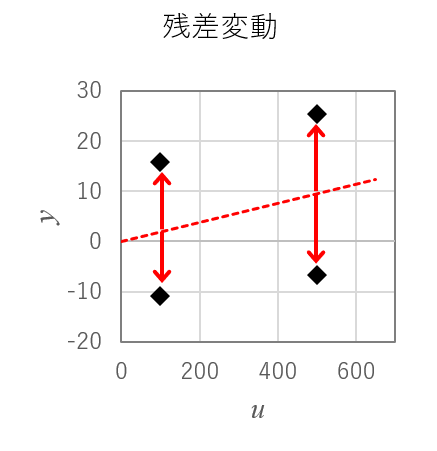
残差変動とは、回帰直線から各実験データまでの変動のことです。

残差変動は、全変動の内、回帰変動ではない成分とも言うことができ、残差変動\(S_E\)は以下の式で計算されます。

$$S_E=S_T-S_{\beta}$$

残差変動は、「ノイズによる変動」と考えることができます。
なお、残差変動には、ランダムノイズや読み取り誤差などの成分も含まれることになります（今回はシミュレーションなので、これらの成分は極めて小さくなります）。

SN比の計算手順

変動分解の結果からSN比を計算します。
SN比\(\eta\)は、回帰変動\(S_{\beta}\)と残差変動\(S_E\)の比率の常用対数を10倍した値となります。

$${\eta}=10\log_{10}{\frac{S_{\beta}}{S_E}}$$

分母に残差変動を取っているため、ノイズによる変動が小さい（ロバスト性が良い）とSN比は大きくなります。
また、対数を取っているのは、後述する水準平均の計算の際に足し算を多用するので、加法性を得るためです。

実際に、サンプルNo.1について計算をしてみます。

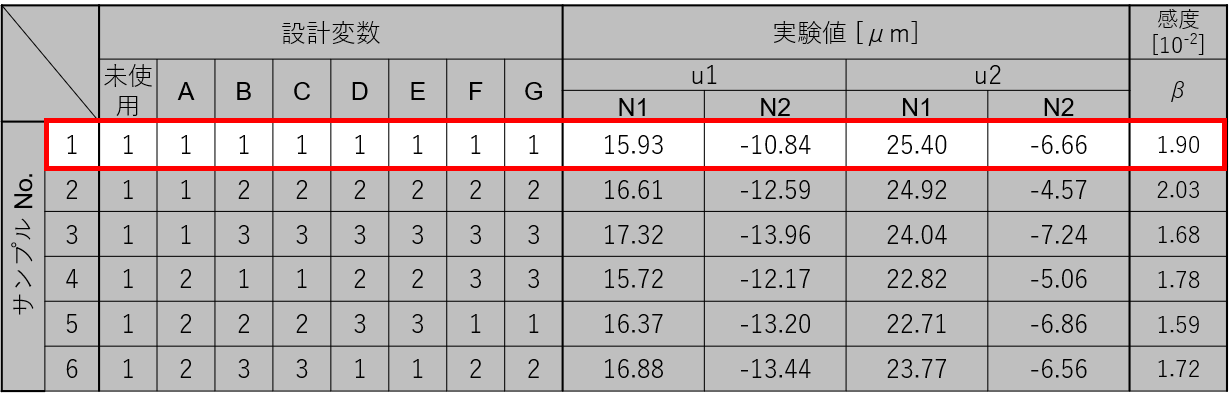
$$S_T=\sum_{i=1}^{2}{\sum_{j=1}^{2}{{y_{ij}}^2}}={15.93}^2+{(-10.84)}^2+{25.40}^2+{(-6.66)}^2=1060.79$$

$$S_{\beta}=2\sum_{i=1}^{2}{({{\beta}u_{i}})^2}=2\times\left\{(1.90\times10^{-2}\times100)^2+(1.90\times10^{-2}\times500)^2\right\}=187.69$$

$$S_E=S_T-S_{\beta}=1060.79-187.69=873.10$$

$${\eta}=10\log_{10}{\frac{S_{\beta}}{S_E}}=10\log_{10}{\frac{187.69}{873.10}}=-6.68 [\text{db}]$$

以上の計算を他の行についても同様に行います。

ちなみに、SN比の単位に\([\text{db}]\)と書きましたが、これは「デシベル」と呼びます。信号解析で用いられるSN比の単位も「デシベル」ですが、こちらは\([\text{dB}]\)です。表記を小文字にしているのは、信号解析のSN比と区別するため慣例的にそうしているためです。

感度・SN比を直交表のすべての行について計算した結果、以下のようになりました。

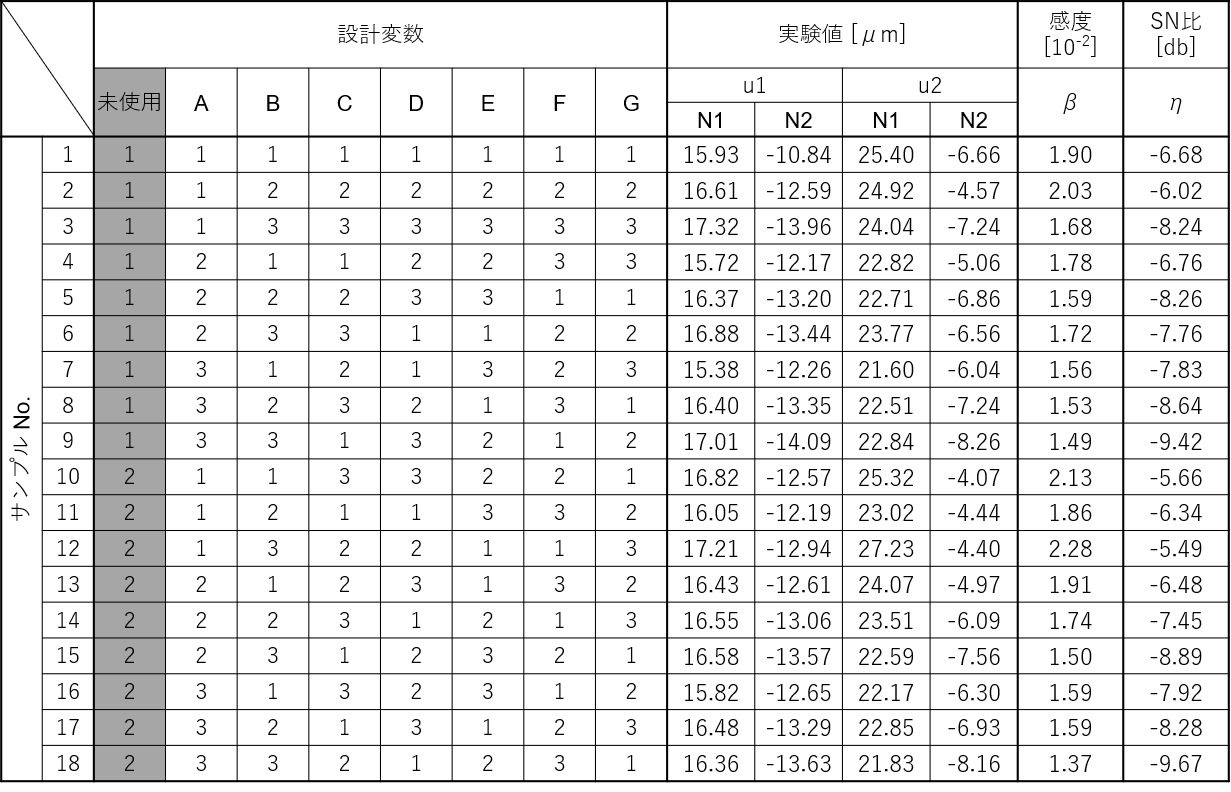
要因効果図の作成

要因効果図は、各々の設計変数の水準を変えたときに、感度とSN比がどれだけ変化するのか視覚的に表すグラフです。
このグラフを描くために、まずは各設計変数の水準平均を計算します。

水準平均の計算

水準平均は、各設計変数ごとに第1～3の水準それぞれについて、感度とSN比の平均値を計算することによって求められます。これは直交表を利用することで簡単に計算ができます。
以下は、設計変数Aの第1水準の水準平均についての例です。

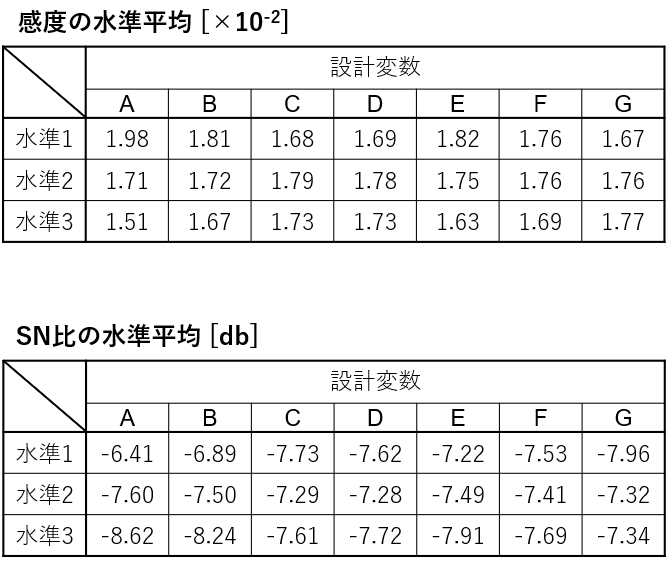
同様にして、すべての設計変数のすべての水準について水準平均を計算します。以下表がその結果です。

要因効果図の作成

要因効果図は上記の水準平均をプロットしたものになります。

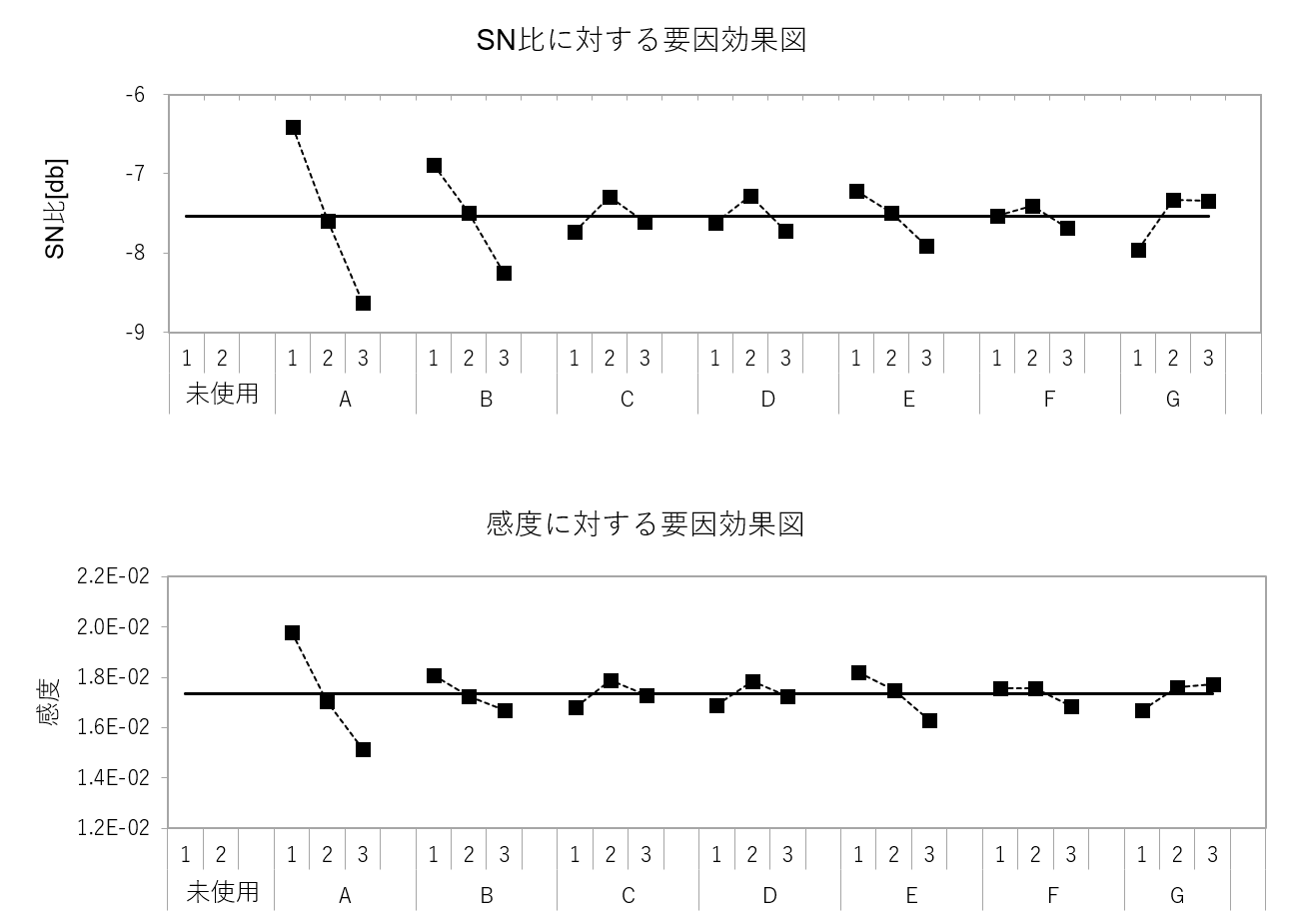
SN比と感度それぞれについてグラフを作成します。両方ともグラフの横軸は2段になっていて、各設計変数（正確には直交表の各列）と水準を表します。そして、縦軸に先ほど計算した水準平均値をプロットしています。太い実線は全サンプルの平均値です。

まとめ

実験データの処理は、以上になります。感度・SN比の計算から要因効果図を描くところまで説明をしました。

本記事に書いていることは、すべてシステマティックに計算できます。設計者の判断などが介在するところは一切ありません。したがって、実務においては計算機にあらかじめプログラムを組み込んで計算させることがほとんどです。計算は比較的簡単なので、Excelで十分です。

しかし、次回はそういうわけには行きません。今回描いた要因効果図から設計者自身が情報を読み取り、判断をしなければならない作業になります。というわけで、いよいよ次回、実際にロバストパラメータ設計を行い、設計の締めを行います。