ロバストパラメータ設計（第五回）
パラメータ水準の決定

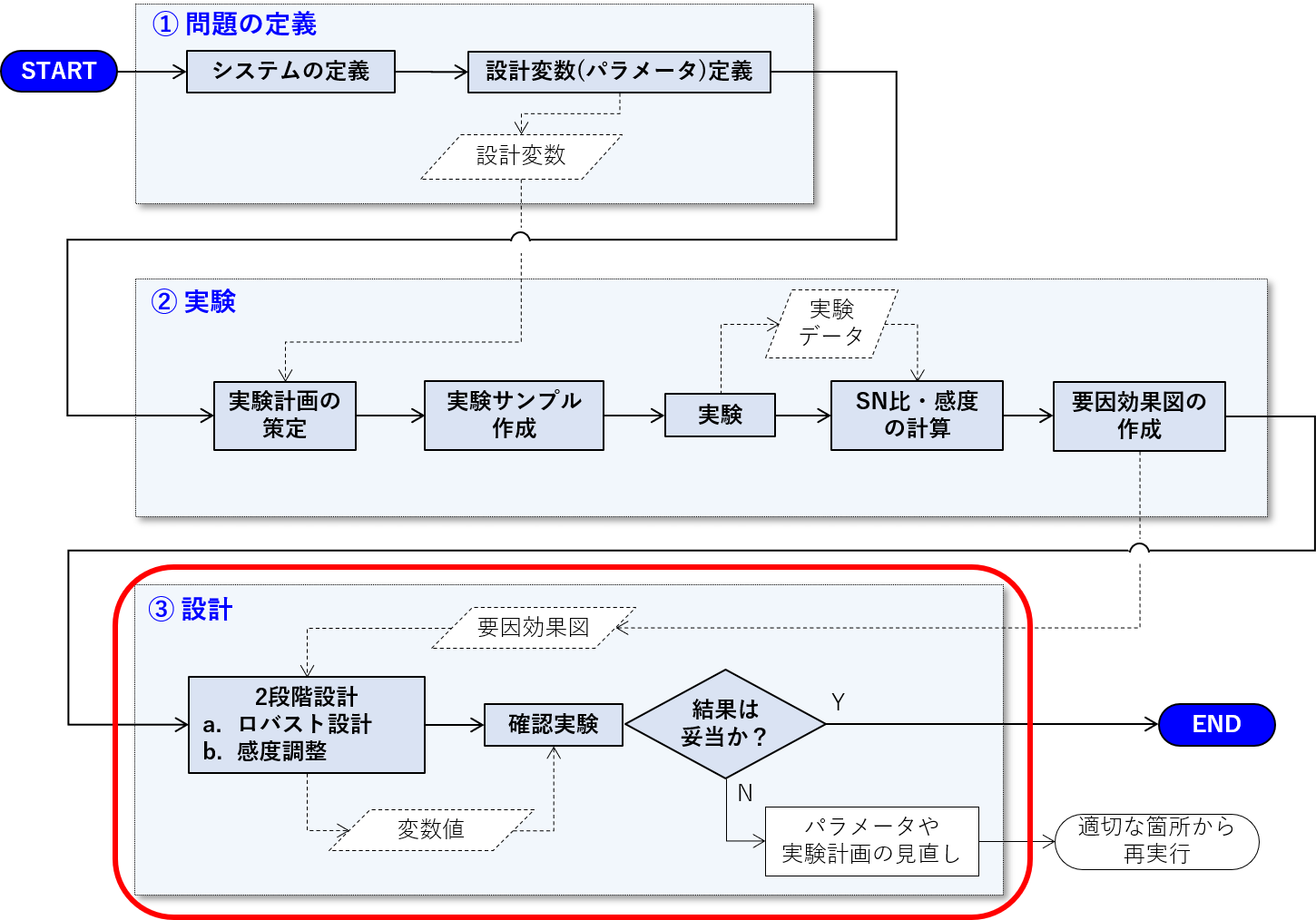
前回まででパラメータ設計のための材料が揃いました。今回は、実際にパラメータの設計を行います。作業フローで示すと、最後のブロックになります。

要因効果図から読み取れること

要因効果図の見方

前回は、下のような要因効果図の作成まで行いました。上段はSN比、下段は感度についてのグラフです。まずは、この図の見方について説明をします。

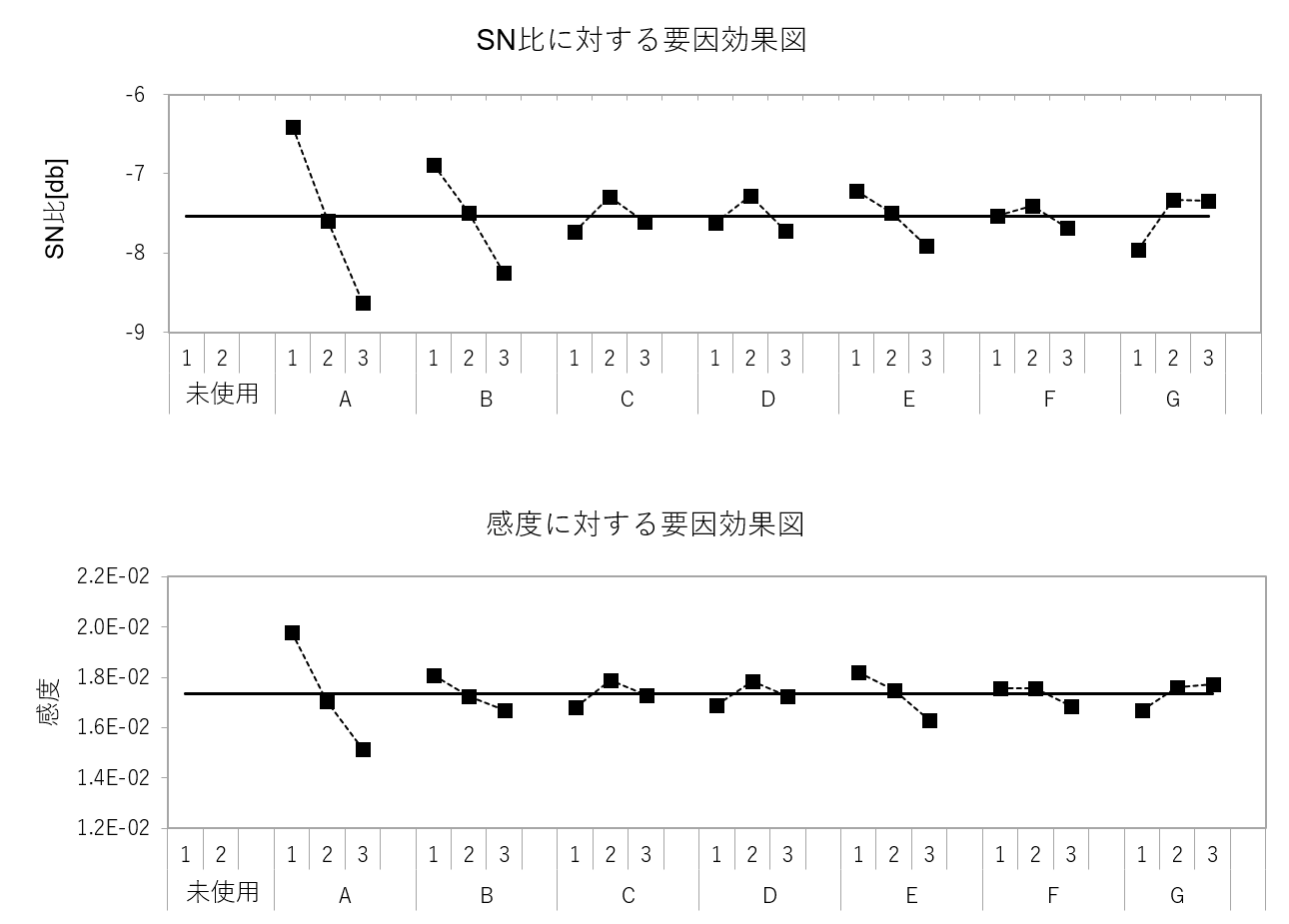
3つの点からなる折れ線が7本あります。7本の折れ線は各設計変数のもので、3つの点は、設計変数の第1～3水準の水準平均値をプロットしたものです。

最初に、縦軸方向に幅の広い設計変数を探します。
縦軸方向の幅は、「水準を変えることによる変化幅」であり、幅が広い設計変数は、結果に与える影響が大きい変数になります。パラメータの設計はこの幅を見て、影響の大きい設計変数から優先的に水準を決定していきます。

水準の選定

ロバストパラメータ設計の2段階設計では、まず、SN比の要因効果図から見ていきます。

SN比の要因効果図で、幅が広い設計変数は、\(A\)と\(B\)です。したがって、\(A・B\)の水準は、SN比が大きくなるように決めます（SN比が大きい方がロバスト性は高いことは前回記事を参照）。
今回の事例では、\(A=1, B=1\)です。残りの設計変数はあまり影響は高くなさそうですが、とりあえずSN比が最大を示している水準にしておきます。

次に、感度に対する要因効果図を見ます。見方はSN比のものと同じです。
今回の所望特性は、「感度を低く」でした。したがって、縦軸方向幅が広い設計変数から優先的に、感度が低くなる水準を選定します。
感度については、\(A\)が影響が大きそうです。感度が低くなる\(A=3\)を選択し、残りもとりあえず、感度が最小となる水準を選択しておきます。

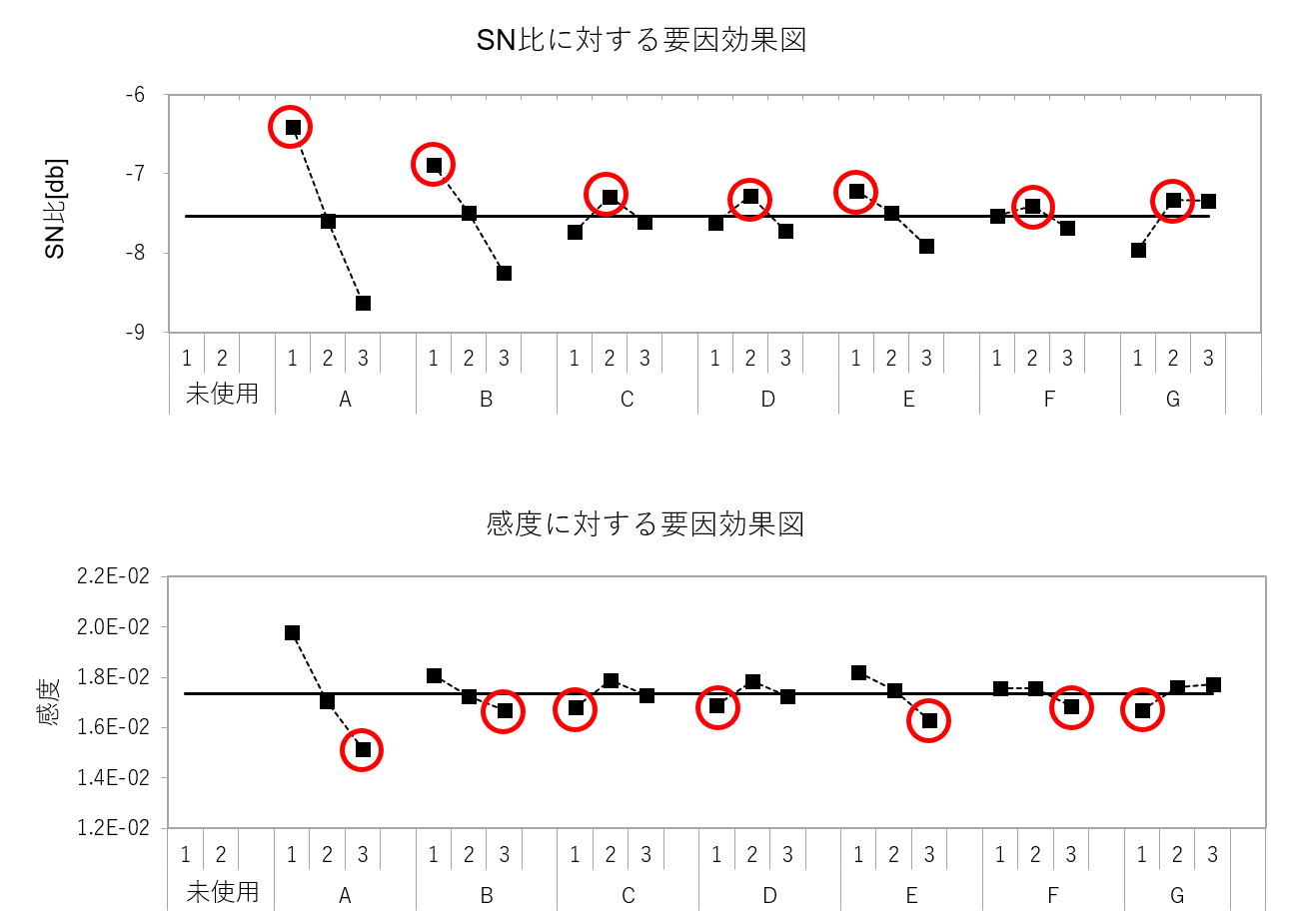
このように、「ロバスト性を確保した状態で、所望特性を得る」手順でパラメータを決める方法が「2段階設計」と呼ばれる所以です。

しかし、ここで困ったことになりました。選択した水準を見てください。SN比と感度で、選択水準が一致していません。
そもそも各設計変数の折れ線の形をよく見ると、「SN比を高く、感度を低く」という選択はできないことが分かります。

どうするか?

タグチメソッドに関する書籍では、「ロバスト性を確保した状態で、所望特性を得る」ということが基本事項として書かれています。
今回の設計対象では、教科書通りの手順では答えは得られないことになります。
このようなことに出くわすと、よく「タグチメソッドは使えない」などと考える設計者がいます。
しかし、それは教科書の手順が悪いのではないと、私は思います。

タグチメソッドはあくまで「技法」であって、結果を保証するものではありません。結果を保証するのは、設計者自身です。
なので、ここで「タグチメソッドは通用しない」と判断して別の方法に移るのも自由です。しかし、それではここまでの時間が無駄になりますし、そもそもその別の方法というのも、どうすればいいのか全く分かりません。
よって、今回の結果をもう少しよく考えてみることにします。

回帰変動と残差変動で見てみる

そもそも、SN比の計算式をよく見てみましょう。

$${\eta}=10\log_{10}{\frac{S_{\beta}}{S_E}}$$

SN比は残差変動\(S_{E}\)と回帰変動\(S_{\beta}\)から計算されます。
回帰変動は、入出力の比例特性による変動です。つまり、比例係数である感度と密接に関係しています。具体的には、感度が大きいほど回帰変動は大きくなります。
SN比では、分子に回帰変動を取っているので、残差変動が変わらないとすると、「感度が大きくなるとSN比は大きく」なります。所望特性とは逆です。
このことから、今回の設計対象においては、SN比の計算式に原因がありそうです。

そこで、SN比を用いずに、回帰変動と残差変動で見てみることにします。
残差変動は、前回記事で「ノイズによる変動」と説明しました。したがって、これでもロバスト性の評価はできそうです。また、上記から回帰変動で感度の評価もできそうです。

残差変動と回帰変動で要因効果図を描くと下のようになります。赤丸は、残差変動小・回帰変動小になる水準を機械的に選定したものです。

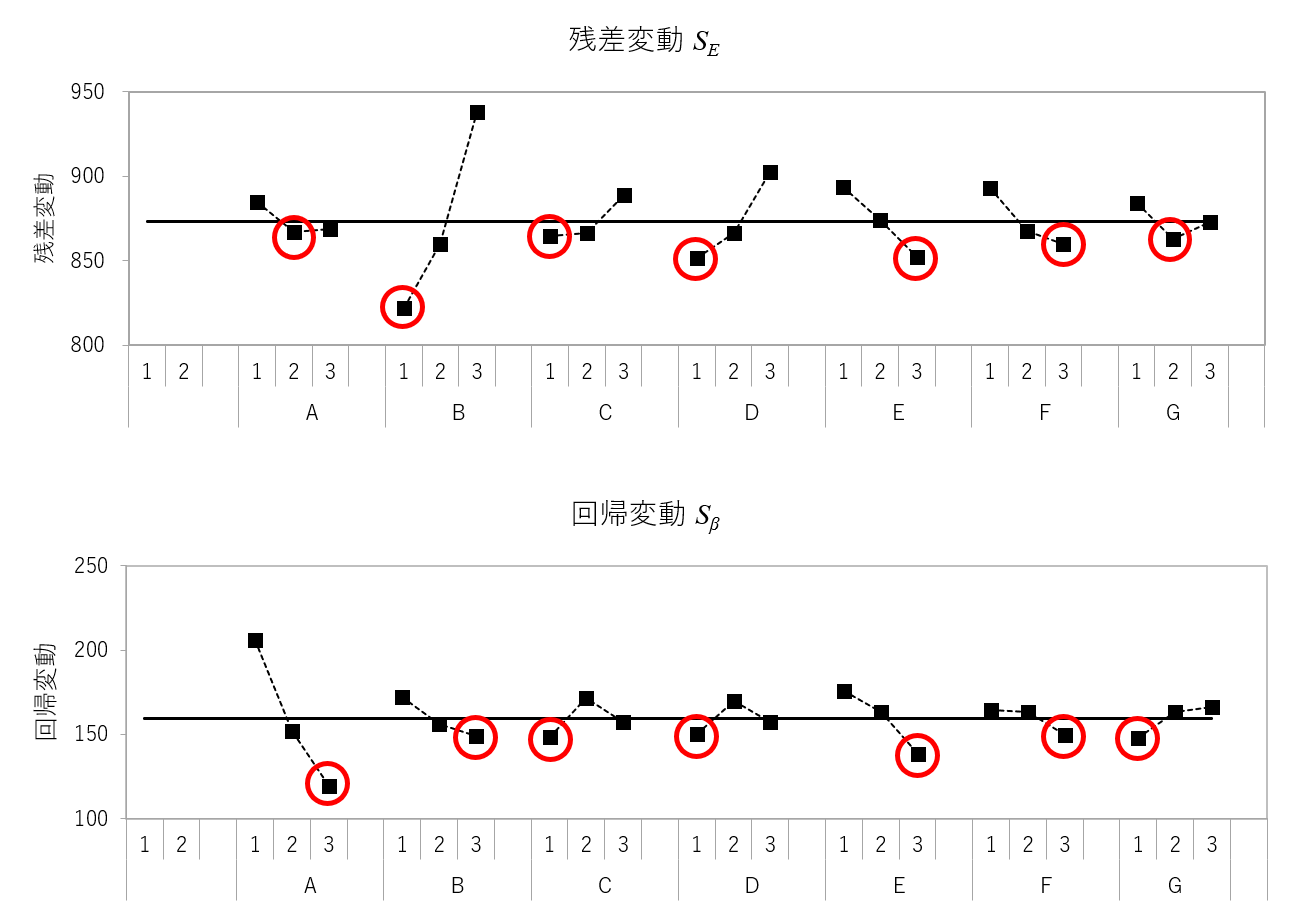
縦軸方向幅を確認すると、残差変動に大きく影響を与えるのは\(B\)、回帰変動に大きく影響を与えるのは\(A\)と読み取れます。今回は上手く分かれてくれました。

最終的に、\(A\)と\(B\)をそれぞれ水準3、水準1に選択します。また、\(C～F\)は赤丸の通りに選択し、\(G\)は水準1としました。

確認実験

選択した水準でモデルを作成（設計モデル）し、これまでと同様の実験（シミュレーション）を実施します。比較用の3モデルを加えた以下の4モデルで、シミュレーションを実施しました。

モデル	A	B	C	D	E	F	G	説明
設計モデル	3	1	1	1	3	3	1	残差変動・回帰変動の要因効果図を基に水準を選定
中間水準モデル	2	2	2	2	2	2	2	すべての設計変数の水準を中間(2)に選択
SN比優先モデル	1	1	2	2	1	2	2	SN比の要因効果図から、SN比最大になる水準を選択
感度優先モデル	3	3	1	1	3	1	1	感度の要因効果図から、感度最大になる水準を選択

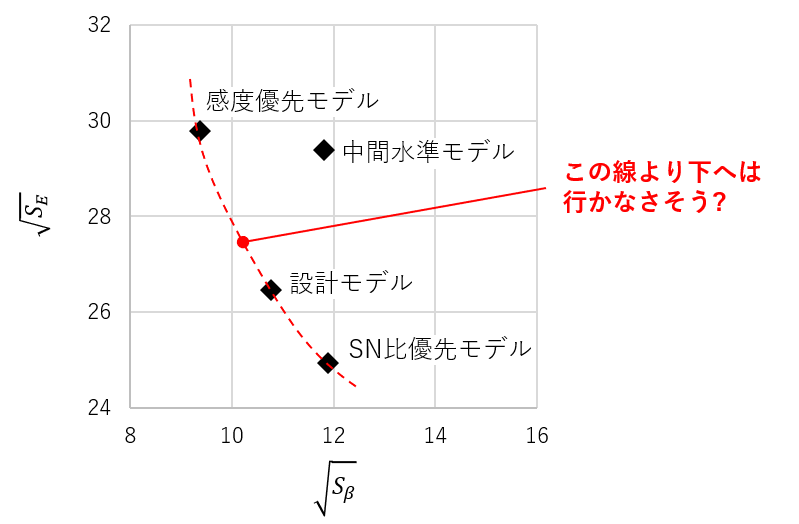
4つのモデルのシミュレーション結果から回帰変動と残差変動を計算し、2次元平面上にプロットしてみます。
なお、回帰変動と残差変動の単位は出力の2乗となっており、イメージしやすくするために、平方根を取ってプロットしました。

設計モデル・SN比優先モデル・感度優先モデルの3つのモデルの関係をイメージしてみましょう。
SN比優先および感度優先モデルは、その名の通りです。一方の特性は良い性能ですが、もう片方は悪化します。
設計モデルは、そのバランスを取ったモデルと言えそうです。

ここから先は深読みになります。点が3つしかないので確かなことは言えませんが、回帰変動（感度）と残差変動（ロバスト性）には、図中の赤い破線のような関係がありそうです。つまり、この2つは同時に最小値を取ることはできない関係にありそうと推測されます。このような関係は、「多目的設計問題」で出てきます。今回はそこまで説明しませんが、いずれ記事にしようと思っています。

設計の締め

設計者の仕事はこれで終わりではありません。
上記のような考察（深読み）ができれば、設計モデルのみならず、感度優先モデルやロバスト性優先モデルも提案することができます。
さらに、更なる性能向上を狙う指針にもつなげることができます。例えば、「感度優先モデルをベースにしてロバスト性を上げるために追加設計をする」とか。各シミュレーションの結果をより詳細に分析すれば、何かヒントがつかめるかもしれません。

どこまで行うかは、設計の要求や仕様によります。設計者は、これらを勘案して「設計の解」を決めなければなりません。

まとめ

5回の記事にわたり、タグチメソッドのロバストパラメータ設計について説明しました。

デモ問題では、セオリー通りに行きませんでしたが、私の経験上、設計実務ではむしろセオリー通りに行くことの方が少ないです。

大切なのは、セオリーを評価するのではなくて、自身の設計内容を評価することです。
経験がないとなかなか難しいですが、基本を押さえていれば必ず何かしらの「解」に辿り着けるはずです。

---